Tag: physics
Claude Shannon – Father of Information Theory
This summer in the Complex Systems Advanced Academic Workshop we are devoting attention to information theory. In collecting some materials about Claude Shannon, I came across the above video and thought I would share it with others. Here is the description … “Considered the founding father of the electronic communication age, Claude Shannon’s work ushered in the Digital Revolution. This fascinating program explores his life and the major influence his work had on today’s digital world through interviews with his friends and colleagues.”
NetSci 2010 — MIT Media Lab
Tomorrow is the first day of presentations at NetSci2010. Our paper will presented in AM Network Measures Panel. Anyway, for those interested in leveraging network science to study the dynamics of large social and physical systems — the conference promises a fantastic lineup of speakers. Check out the program!
A Quantum Calculation: Is Information at the Root of Everything?
From the article “… Vlatko Vedral, an Oxford physicist, examines the claim that bits of information are the universe’s basic units, and the universe as a whole is a giant quantum computer. He argues that all of reality can be explained if readers accept that information is at the root of everything.”
Detrending Career Statistics in Professional Baseball: Accounting for the Steroids Era and Beyond
From the abstract: “There is a long standing debate over how to objectively compare the career achievements of professional athletes from different historical eras. Developing an objective approach will be of particular importance over the next decade as Major League Baseball (MLB) players from the “steroids era” become eligible for Hall of Fame induction. Here we address this issue, as well as the general problem of comparing statistics from distinct eras, by detrending the seasonal statistics of professional baseball players. We detrend player statistics by normalizing achievements to seasonal averages, which accounts for changes in relative player ability resulting from both exogenous and endogenous factors, such as talent dilution from expansion, equipment and training improvements, as well as performance enhancing drugs (PED). In this paper we compare the probability density function (pdf) of detrended career statistics to the pdf of raw career statistics for five statistical categories — hits (H), home runs (HR), runs batted in (RBI), wins (W) and strikeouts (K) — over the 90-year period 1920-2009. We find that the functional form of these pdfs are stationary under detrending. This stationarity implies that the statistical regularity observed in the right-skewed distributions for longevity and success in professional baseball arises from both the wide range of intrinsic talent among athletes and the underlying nature of competition. Using this simple detrending technique, we examine the top 50 all-time careers for H, HR, RBI, W and K. We fit the pdfs for career success by the Gamma distribution in order to calculate objective benchmarks based on extreme statistics which can be used for the identification of extraordinary careers.”
On the Stability of Community Detection Algorithms on Longitudinal Citation Data: Paper & New Code
Last summer, Dan, Jon and I wrote our conference paper for ASNA 2009 entitled On the Stability of Community Detection Algorithms on Longitudinal Citation Data. The purpose of this paper was to experimentally explore a number of properties of community detection algorithms, especially as applied to citation networks (c.f. Supreme Court, Tax Court, United States Code).
The model is a fairly simple discrete-time directed growing graph. At time 0, we create a completely disconnected graph with some initial number of vertices. The number of new vertices after time 0 is then modeled by a homogeneous Poisson process. For each of these new vertices, we also model the number of edges per vertex as IID Poisson distributions. The probability distribution over these edges is specified by a modified preferential attachment mechanism.
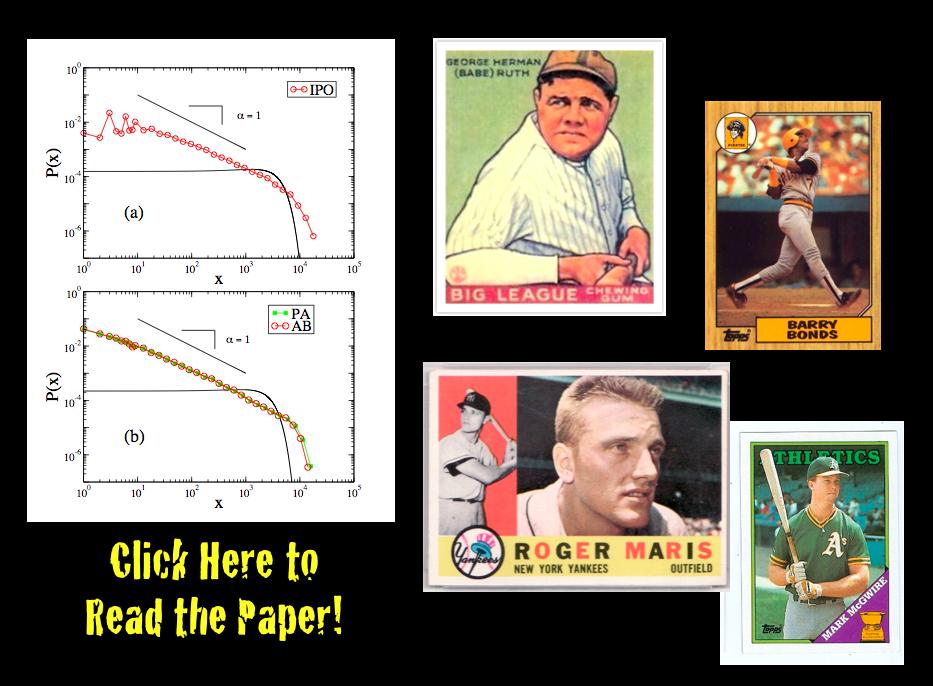
Most of our questions consider what we’ve called the average pairwise stability. This can be thought of as answering the following question: “what is the probability that Alice and Bob are friends tomorrow if they were friends today?” Here, friendship corresponds to sharing the same community. By asking this question for all pairs of vertices (dyads) for all time steps in which both vertices existed, we get a probability that a community dyad is preserved from step to step. It is important to note that we’re not claiming all algorithms applied to all systems should have high average pairwise stability. In fact, for systems that involve dynamics like random rewiring, the only way to get high pairwise stability is to put all vertices in the same community or their own community at all steps – obviously trivial and unhelpful solutions in practice.
Given this model and this conception of stability, we want to perform the following experiments:
- How do the edge-betweenness, fast greedy, and leading eigenvector community detection algorithms compare in terms of their average pairwise stability…
- for varying levels of preferential attachment?
- for varying vertex and edge rates?
- Is there a significant tradeoff between the number of communities and the average pairwise stability of these community detection algorithms?
The answers are yes, yes, and yes! You should read the paper for more details.
I’ve also produced some code to help you assess the average pairwise stability for your dataset. The code requires igraph and is only in Python at this point due to an issue with R’s vertex label handling (which I can hopefully work around). You can get the average pairwise stability methods on github and check out the example below:
The Age of Quantum Computing? [From Nature]
From the Abstract … “The race is on to build a computer that exploits quantum mechanics. Such a machine could solve problems in physics, mathematics and cryptography that were once thought intractable, revolutionizing information technology and illuminating the foundations of physics. But when?” (Subscription may be required for Access)
“Sink Method” Poster for Conference on Empirical Legal Studies (CELS 2009 @ USC)
As we mentioned in previous posts, Seadragon is a really cool product. Please note load times may vary depending upon your specific machine configuration as well as the strength of your internet connection. For those not familiar with how to operate it please see below. In our view, the Full Screen is best the way to go ….
Algorithmic Community Detection in Networks
Community detection in networks is an extremely important part of the broader network science literature. For quite a while, we have meant to highlight the extremely useful review article written by Mason Porter (Oxford) Jukka-Pekka Onnela (Harvard/Oxford) and Peter J Mucha (UNC). Rather than offer our description of the article, we thought it best to highlight commentary on the subject provided by the authors.
For example, in describing the paper over at Harvard’s Complexity and Social Networks Blog Jukka-Pekka Onnela posted the following… “Uncovering the “community” structure of social networks has a long history, but communities play a pivotal role in almost all networks across disciplines. Intuitively, one can think of a network community as consisting of a group of nodes that are relatively densely connected to each other but sparsely connected to other dense groups of nodes. Communities are important because they are thought to have a strong bearing on functional units in many networks. So, for example, communities in social networks can correspond to different social groups, such as family, whereas web pages dealing with a given subject tend to form topical communities. The concept is simple enough, but it turns out that coming up with precise mathematical definitions and algorithms for community detection is one of the most challenging problems in network science. Recently, a lot of the research in this area has been done using ideas from statistical physics, which has an arsenal of tools and concepts to tackle the problem. Unfortunately (but understandably) relatively few non-physicists like to read statistical physics papers.”
These scholars quote Mark Newman noting “[T]he development of methods for finding communities within networks is a thriving sub-area of the field, with an enormous number of different techniques under development. Methods for understanding what the communities mean after you find them are, by contrast, still quite primitive, and much needs to be done if we are to gain real knowledge from the output of our computer programs.” They later note “the problem of how to validate and use communities once they are identified is almost completely open.”
Anyway, if you are interested in learning more about this important piece of the network science toolkit … we suggest you read this paper!