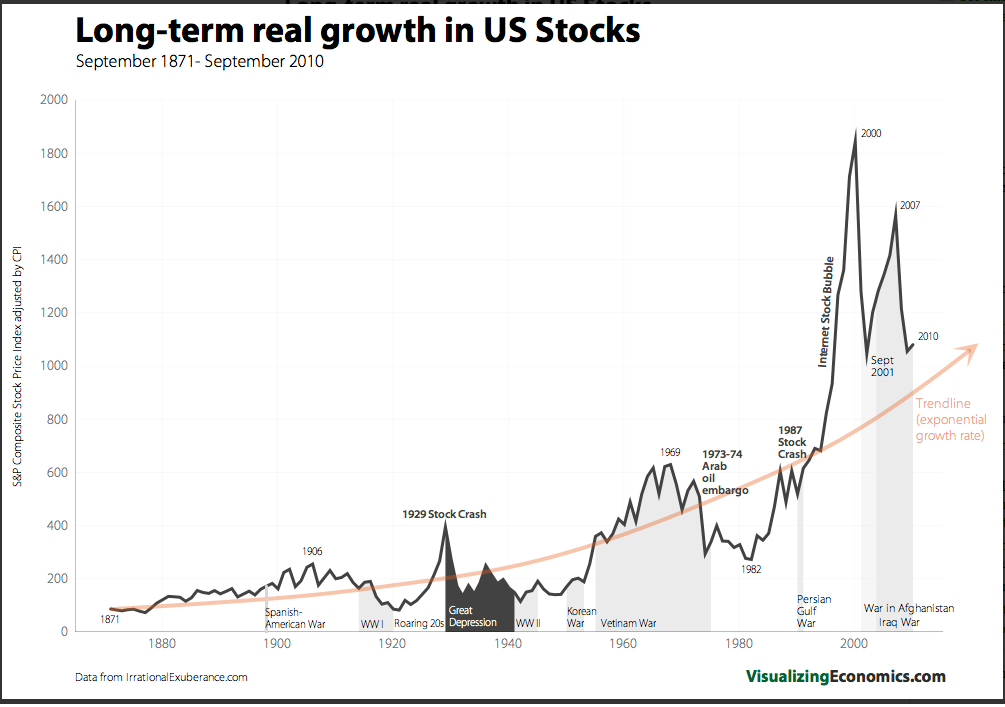
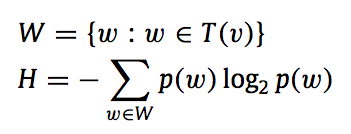If you would like to see this chart plotted on a log scale click here. Also, Visualizing Economics has a number of other very interesting projects worth checking out.
Month: October 2010
Introduction to Computing for Complex Systems — ICPSR 2010 — My Full Course Slides Available Online!
I am going to bump this post to front of the blog one last time as there has been some interest in this material. It has now been several weeks since we completed the full four week class here at the ICPSR Program in Quantitative Methods. In this course, I (together with my colleagues) highlight the methods of complex systems as well as several environments designed to explore the field. These include Netlogo (agent based models and network models), Vensim (system dynamics / ecological modeling) and Pajek (empirical network analysis). In the final week, we cover a variety of advanced topics:
- (a) Community Detection in Networks
- (b) Computational Linguistics / Natural Language Processing
- (c) Diffusion Models and Mathematical Modeling with Data
- (d) Exponential Random Graph (p*) Models
- (e) Information Retrieval / Webscraping
Although, we do not work with more advanced languages within the course, those who need to conduct complex analysis are directed to alternatives such as R, Python, Java, etc.
Anyway, the slides are designed to be fully self-contained and thus allow for individually paced study of the relevant material. If you work through the slides carefully you should be able to learn the software as well as many of the core principles associated with the science of complex systems. The material should be available online indefinitely. If you have questions, feel free to email me.
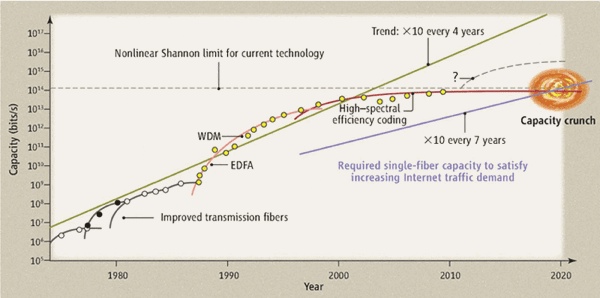
“Peak Data” or “The Capacity Crunch” [From Science]
From this week’s issue of Science comes Filling the Light Pipe by David J. Richardson. This is an important article highlighting a serious challenge facing the both the scientific and policy community.
From the abstract: “It has been a landmark year for the field of optical telecommunications, with the award of the 2009 Nobel Prize to Charles Kao for his insight in the mid-1960s that the future of communications lay in single-mode silica-based optical fibers (1) as well as the 50th anniversary of the first demonstration of the laser—both key technologies responsible for the development of the global-scale communications networks of today (2). Recently, however, a growing realization has emerged within the telecommunications industry that the end of the phenomenal growth in optical fiber communication capacity is within sight. At this year’s Optical Fiber Communication Conference (OFC 2010), several groups reported results within a factor of 
2 of the ultimate capacity limits of existing optical fiber technology. Without radical innovation in our physical network infrastructure—that is, improvements in the key physical properties of transmission fibers and the optical amplifiers that we rely on to transmit data over long distances—we face what has been widely referred to as a “capacity crunch” that could severely constrain future Internet growth, as well as having social and political ramifications.”
[HT to Paul Kedrosky]
How Long is the Coastline of the Law: Additional Thoughts on the Fractal Nature of Legal Systems
Do legal systems have physical properties? Considered in the aggregate, do the distinctions upon distinctions developed by common law judges self-organize in a manner that can be said to have definable physical property (at least at a broad level of abstraction)? The answer might lie in fractal geometry.
Fractal geometry was developed in a set of classic papers by mathematician Benoît Mandelbrot. The original paper in the field How Long is the Coastline of Britain describes the coastline measurement problem. In short form, the length of the coast line is a function of the size of measurement one employs. As shown below, as the unit of measurement decreases the length of the coastline increases. The ideas expressed in this and subsequent papers have been applied to a wide class of substantive questions. In particular, the application to economic systems has been particularly illuminating. Given recent economic events, we agree with views of the Everyday Economist arguing the applied economic theory built upon his work should earn Mandelbrot a share of the Nobel Prize.
A more abstract fractal is the simple version of the Sierpinski triangle displayed at the top of this post. Here, there exists self similarity at all levels. Specifically, at each iteration of the model, the triangles at the tip of each of the lines replicate into self similar versions of the original triangle. If you click on the visual above, you can run the applet (provided you have java installed on your computer). {Side note: those of you NKS Wolfram fans out there will know the Sierpinski triangle can be generated using cellular automata Rule 90.}
For those who are interested in another demonstration consider the Koch Snowflake — a fractal which also offers a view of the relevant properties. The Koch Snowflake is a curve with infinite length (i.e. there is no convergence even though it is located in a bounded region around the original triangle). Click here to view an online demo of the Koch Snowflake.
So, you might be wondering … what is the law analog to fractals? As a first-order description of one important dynamic of the common law, we believe significant progress can be made by considering the conditions under which legal systems behave in a manner similar to fractals. For those interested, a number of important papers have discussed the fractal nature of legal systems. While discussing legal argumentation, the original idea is outlined in two important early papers The Crystalline Structure of Legal Thought and The Promise of Legal Semiotics both by Jack Balkin. The empirical case began more than ten years ago in the important paper How Long is the Coastline of the Law? Thoughts on the Fractal Nature of Legal Systems by David G. Post & Michael B. Eisen. It continues in more recent scholarship such as The Web of the Law by Thomas Smith.
In our view, the utility of this research is not to adjudicate the common law to be a fractal. Indeed, there exist mechanisms which likely prevent legal systems from actually behaving as unbounded fractal. The purpose of the discussion is determine whether describing law as a fractal is a reasonable first-order description of at least one dynamic within this complex adaptive system. While full adjudication of these questions is still an area of active research, we highlight these ideas for their important potential contribution to positive legal theory.
One thing we want to flag is the important relationship between the power law distributions we discussed in these prior posts (here and here) and the original work of Benoît Mandelbrot. The mapping of the power law like properties displayed by the common law and its constitutive institutions is part of the larger empirical case for the fractal nature of legal systems. Building upon the prior work, in two recent papers, which are available on SSRN here and here, we mapped this property of self organization among two sets of legal elites — judges and law professors.
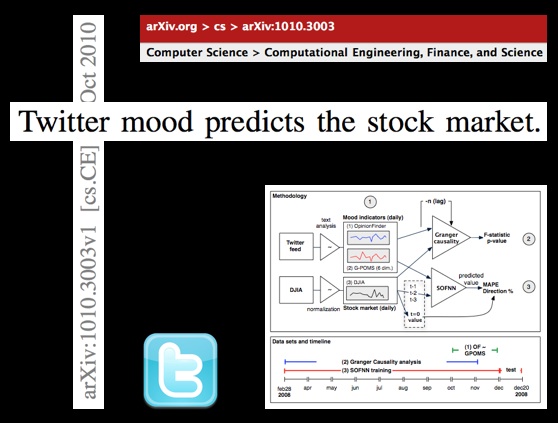
Twitter Mood Predicts the Stock Market
From the physics arXiv comes the interesting paper entitled Twitter mood predicts the stock market. Mike has additional information on the paper over at ETF Central. However — for those who might be interested — here is the abstract:
“Behavioral economics tells us that emotions can profoundly affect individual behavior and decision-making. Does this also apply to societies at large, i.e., can societies experience mood states that affect their collective decision making? By extension is the public mood correlated or even predictive of economic indicators? Here we investigate whether measurements of collective mood states derived from large-scale Twitter feeds are correlated to the value of the Dow Jones Industrial Average (DJIA) over time. We analyze the text content of daily Twitter feeds by two mood tracking tools, namely OpinionFinder that measures positive vs. negative mood and Google-Profile of Mood States (GPOMS) that measures mood in terms of 6 dimensions (Calm, Alert, Sure, Vital, Kind, and Happy). We cross-validate the resulting mood time series by comparing their ability to detect the public’s response to the presidential election and Thanksgiving day in 2008. A Granger causality analysis and a Self-Organizing Fuzzy Neural Network are then used to investigate the hypothesis that public mood states, as measured by the OpinionFinder and GPOMS mood time series, are predictive of changes in DJIA closing values. Our results indicate that the accuracy of DJIA predictions can be significantly improved by the inclusion of specific public mood dimensions but not others. We find an accuracy of 87.6% in predicting the daily up and down changes in the closing values of the DJIA and a reduction of the Mean Average Percentage Error by more than 6%.”
Measuring the Complexity of the Law : The United States Code [Repost]
Understanding the sources of complexity in legal systems is a matter long considered by legal commentators. In tackling the question, scholars have applied various approaches including descriptive, theoretical and, in some cases, empirical analysis. The list is long but would certainly include work such as Long & Swingen (1987), Schuck (1992), White (1992), Kaplow (1995), Epstein (1997), Kades (1997), Wright (2000), Holz (2007) and Bourcier & Mazzega (2007). Notwithstanding the significant contributions made by these and other scholars, we argue that an extensive empirical inquiry into the complexity of the law still remains to be undertaken.
While certainly just a slice of the broader legal universe, the United States Code represents a substantively important body of law familiar to both legal scholars and laypersons. In published form, the Code spans many volumes. Those volumes feature hundreds of thousands of provisions and tens of millions of words. The United States Code is obviously complicated, however, measuring its size and complexity has proven be non-trivial.
In our paper entitled, A Mathematical Approach to the Study of the United States Code we hope to contribute to the effort by formalizing the United States Code as a mathematical object with ahierarchical structure, a citation network and an associated text function that projects language onto specific vertices.
In the visualization above, Figure (a) is the full United States Code visualized to the section level. In other words, each ring is a layer of a hierarchical tree that halts at the section level. Of course, many sections feature a variety of nested sub-sections, etc. For example, the well known 26 U.S.C. 501(c)(3) is only shown above at the depth of Section 501. If we added all of these layers there would simply be additional rings. For those interested in the visualization of specific Titles of the United States Code … we have previously created fully zoomable visualizations of Title 17 (Copyright), Title 11 (Bankruptcy), Title 26 (Tax) [at section depth], Title 26 (Tax) [Capital Gains & Losses] as well as specific pieces of legislation such as the original Health Care Bill — HR 3962.
In the visualization above, Figure (b) combines this hierarchical structure together with a citation network. We have previously visualized the United States Code citation network and have a working paper entitled Properties of the United States Code Citation Network. Figure (b) is thus a realization of the full United States Code through the section level.
With this representation in place, it is possible to measure the size of the Code using its various structural features such as vertices V and its edges E. It is possible to measure the full Code at various time snapshots and consider whether the Code is growing or shrinking. Using a limited window of data, we observe growth not only in the size of the code but also its network of dependancies (i.e. its citation network).
Of course, growth in the size United States Code alone is not necessarily analogous to an increase in complexity. Indeed, while we believe in general the size of the code tends to contribute to “complexity,” some additional measures are needed. Thus, our paper features structural measurements such as number of sections, section sizes, etc.
In addition, we apply the well known Shannon Entropy measure (borrowed from Information Theory) to evaluate the “complexity” of the message passing / language contained therein. Shannon Entropy has a long intellectual history and has been used as a measure of complexity by many scholars. Here is the formula for Shannon entropy:
For those interested in reviewing the full paper, it is forthcoming in Physica A: Statistical Mechanics and its Applications. For those not familiar, Physica A is a journal published by Elsevier and is a popular outlet for Econophysics and Quantitative Finance. A current draft of the paper is available on the SSRN and the physics arXiv.
We are currently working on a follow up paper that is longer, more detailed and designed for a general audience. Even if you have little or no interest in the analysis of the United States Code, we hope principles such as entropy, structure, etc. will prove useful in the measurement of other classes of legal documents including contracts, treaties, administrative regulations, etc.
Sebastian Seung: I Am My Connectome [ TED 2010 ]
Sebastian Seung is mapping a massively ambitious new model of the brain that focuses on the connections between each neuron. He calls it our “connectome,” and it’s as individual as our genome — and understanding it could open a new way to understand our brains and our minds.