Month: April 2010
Six Degrees of Marbury v. Madison : A Sink Based Visualization
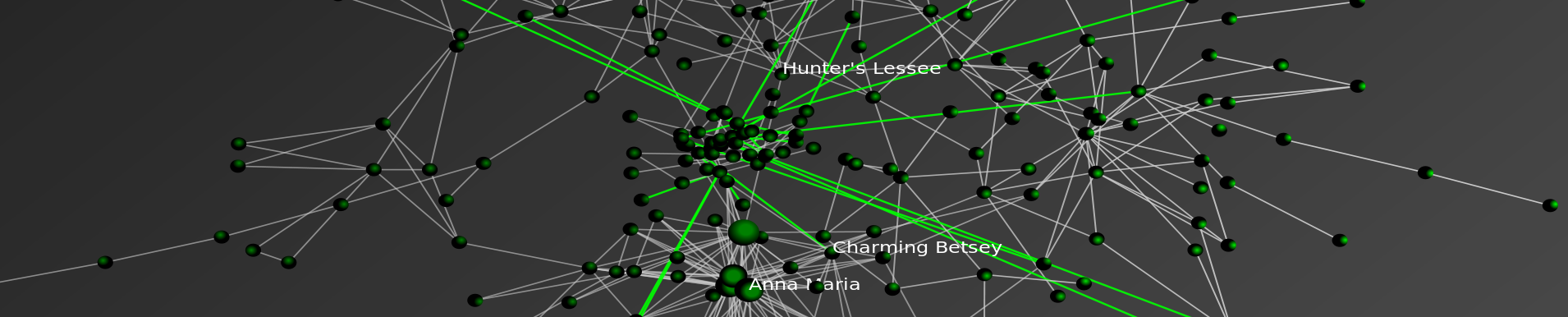
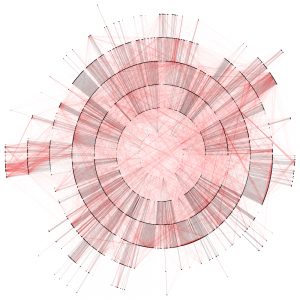
The visualization above is something we call “six degrees” of Marbury v. Madison. It was originally produced for use in our paper Distance Measures for Dynamic Citation Networks. Due to space considerations, we ended up leaving it on the cutting room floor. However, the visual is designed to highlight the idea of a “sink.”
Sinks are one of the core concepts which we outline in our Distance Measures for Dynamic Citation Networks paper. Looking through the prism of a citation network, sinks are the root to which a given legal concept, academic idea or patent based innovation can be drawn. From each citation in a non-sink node, it is possible to trace the chains of citations back to their root (which we call a sink). In the visualization above, the root or sink node is the famed United States Supreme Court decision Marbury v. Madison. Starting from the center and working out to the edge, the first ring are cases that directly cite Marbury v. Madison. The next ring are cases which cite cases that cite Marbury v. Madison. The next ring are cases which cite cases which cases that cite Marbury v. Madison and so on…
Anyway, one of the major contributions of the Distance Measures for Dynamic Citation Networks paper is that it allows us to use these sinks to create pairwise distance/similarity measure between the ith and jth unit. In this instance, the units in this directed acyclic network are the ith and jth decisions of the United States Supreme Court.
Now, it is important to note cases contain many citations and thus can be oriented relative to many different sinks. So, even if a case can be traced to the Marbury sink – this does not preclude it from being traced to other sinks as well. Also, it is possible to design many mathematical functions to characterize the sink based distance between units. For instance, the importance of a sink might decay as its shortest path length increases. An alternative measure might weight the importance of each sinks by the number of unique ancestors shared between nodes i and j that are descended from a given sink of interest. Indeed, many fine-grained choices are possible but they require justification drawn from the given substantive problem …
A Quantum Calculation: Is Information at the Root of Everything?
From the article “… Vlatko Vedral, an Oxford physicist, examines the claim that bits of information are the universe’s basic units, and the universe as a whole is a giant quantum computer. He argues that all of reality can be explained if readers accept that information is at the root of everything.”
Law as a Complex Adaptive System Syllabus -Updated Version 04.24.10
For the past year, Mike and I have been running an undergraduate independent study course entitled Law as a Complex System? Well, it is the end of the academic year here at Michigan and we thought it would be a good idea to sit down and reflect upon the course content. We have made a few important changes to the syllabus and thought we would share the new version with anyone who might be interested. We are really quite happy with where it now stands…
The United States Code — The Movie — Featuring Title 16 — Conservation
Above is a movie displaying Title 16 (Conservation) a subset of the content contained within the United States Code. At more than 2,400 pages (download it here), Title 16 is one of the larger titles in the US Code. Yet, it is not the largest. For example, Title 26 (Internal Revenue Code) and Title 42 (Public Health and Welfare) are far larger than the object displayed above.
Now, you might be wondering why we chose to generate this movie. We envisioned at least two purposes.
(1) The title of this blog is Computational Legal Studies. One of our major goals to either develop or apply tools that scale to life in the era of Big Data. Given the scope of an object such as the United States Code, it is is clear that a significant class of potential analysis cannot reasonably be undertaken without the use of computational tools. Thus, with respect to developing new insights, we believe computational linguistics, information theory, applied graph theory can be of great use. For those interested, our new paper entitled A Mathematical Approach to the Study of the United States Code offers our initial exploration of the possibilities.
(2) We believe this movie can be a meaningful pedagogical device. Many students enter law school and are dismayed when even in statutory based classes they are not exclusively reviewing the black letter law. Given the scope of this and other large bodies of documents, any model of legal education cannot be exclusively be dedicated to teaching black letter law. Instead, such training is appropriately devoted to a mixture of existing legal rules as well as the development of information acquisition protocols that train students to navigate the relevant landscape.
Ron Eglash on African Fractals [via TED]
Math is beautiful and fractals are among the most elegant objects in all of mathematics. I have to admit that I am a bit obsessed with them. For those who are interested in learning more about fractals … this Ted Talk from 2007 by Ron Eglash offers both a useful overview and an application to African design.
Bursts: The Hidden Pattern Behind Everything We Do
Albert-László Barabási, in his usual creative fashion, has produced an interesting game to help publicize his new book, Bursts: The Hidden Pattern Behind Everything We Do.
Read their description of the game below and check it out if you’re interested!
BuRSTS is a performance in human dynamics, a game of cooperation and prediction, that will gradually unveil the full text of Bursts. In a nutshell, if you register at http://brsts.com, you will be able to adopt one of the 84,245 words of the book. Once you adopt, the words adopted by others will become visible to you — thus as each words finds a parent, the whole book will become visible to the adopters. But if you invite your friends (and please do!) and you are good at predicting hidden content, the book will unveil itself to you well before all words are adopted. We will even send each day free signed copied of Bursts to those with the best scores.
Tax Day: A Mathematical Approach to the Study of the United States Code
April 15th is Tax Day! Unless you’ve filed for an extension or you’re a corporation on your own fiscal year, you’ve hopefully finished your taxes by now!
While you were filing your return, you may have noticed references to the Internal Revenue Code (IRC). The IRC, also known as Title 26, is legal slang for the “Tax Code.” Along with the Treasury Regulations compiled into the Code of Federal Regulations (26 C.F.R.), the Internal Revenue Code contains many of the rules and regulations governing how we can and can’t file our taxes. Even if you prepared your taxes using software like TurboTax, the questions generated by these programs are determined by the rules and regulations within the Tax Code and Treasury Regulations.
Many argue that there are too many of these rules and regulations or that these rules and regulations are too complex. Furthermore, many also claim that the “Tax Code” is becoming larger or more complex over time. Unfortunately, most individuals do not support this claim with solid data. When they do, they often rely on either the number of pages in Title 26 or the CCH Standard Federal Tax Reporter. None of these measures take into consideration the real complexity of the Code, however.
In honor of Tax Day, we’re going to highlight a recent paper that we’ve written that tries to address some of these issues – A Mathematical Approach to the Study of the United States Code. The first point to make is that this paper is a study of the entire United States Code. Title 26, the Tax Code, is actually only one small part of the set of rules and regulations defined in the United States Code. The United States Code as a whole is the largest and arguably most important source of Federal statutory law. Compiled from the legislation and treaties published in the Statutes at Large in 6-year intervals, the entire document contains over 22 million words.
In this paper, we develop a mathematical approach to the study of the large bodies of statutory law and in particular, the United States Code. This approach can be summarized as guided by a representation of the Code as an object with three primary parts:
- A hierarchical network that corresponds to the structure of concept categories.
- A citation network that encodes the interdependence of concepts.
- The language contained within each section.
Given this representation, we then calculate a number of properties for the United States Code in 2008, 2009, and 2010 as provided by the Legal Information Institute at the Cornell University Law School. Our results can be summarized in three points:
- The structure of the United States Code is growing by over 3 sections per day.
- The interdependence of the United States Code is increasing by over 7 citations per day.
- The amount of language in the United States Code is increasing by over 2,000 words per day.
The figure above is an actual image of the structure and interdependence of the United States Code. The black lines correspond to structure and the red lines correspond to interdependence. Though visually stunning, the true implication of this figure is that the United States Code is a very interdependent set of rules and regulations, both within and across concept categories.
If you’re interested in more detail, make sure to read the paper –A Mathematical Approach to the Study of the United States Code. If you’re really interested, make sure to check back in the near future for our forthcoming paper entitled Measuring the Complexity of the United States Code.
The Pace of Evolution Across Fitness Valleys
From the abstract: “How fast does a population evolve from one fitness peak to another? We study the dynamics of evolving, asexually reproducing populations in which a certain number of mutations jointly confer a fitness advantage. We consider the time until a population has evolved from one fitness peak to another one with a higher fitness. The order of mutations can either be fixed or random. If the order of mutations is fixed, then the population follows a metaphorical ridge, a single path. If the order of mutations is arbitrary, then there are many ways to evolve to the higher fitness state. We address the time required for fixation in such scenarios and study how it is affected by the order of mutations, the population size, the fitness values and the mutation rate.”
SEAL 11 @ William & Mary Law School
This weekend we participated in the Society for Evolutionary Analysis in Law (SEAL) annual meeting at William & Mary Law School. For those not already familiar, SEAL is devoted to the integration of the life sciences and social sciences into legal scholarship and teaching. Relevant topics include but are not limited to evolutionary and behavioral biology, cognitive science, complex adaptive systems, economics, evolutionary psychology, primatology, etc. SEAL boasts over 400 members from 30 countries — including the 2009 Economics Nobelist Elinor Ostrom. Anyway, this weekend witnessed a very interesting and exciting set of presentations …. we are looking forward to more great presentations at SEAL 12.
What Computer Science Can Teach Economics …
Above is a link to a new release highlighting Constantinos Daskalakis and his important work. Together with Paul Goldberg and Christos Papadimitriou, Constantinos received the Game Theory and Computer Science Prize for his paper “The Complexity of Computing a Nash Equilibrium.” The prize is awarded once every four years at the World Congress of the Game Theory Society. A shorter and simpler version of the paper is available here.
The question of what computer science can teach social science disciplines such as economics is a constant discussion here at Michigan CSCS. I would say the consensus is that there exists real opportunities for meaningful cross-fertilization. For example, take the results presented in this paper. Now, consider a group of agents/players with ranges of different cognitive limitations and information sets playing all types of different games on a multi-dimensional graphs …. now imagine we did not assume the system in question had a fixed point attractor. Rather, assume we allowed for the possibility of a limit cycle attractor or even a strange attractor. Under such conditions, the richness of the problem might encourage one to put aside their pencil and paper and consider what computation might be able to bring to the problem ….
Data on the Legal Blogosphere [Via the Library of Congress]
From the LOC Website … “The Law Library of Congress began harvesting legal blawgs in 2007. The collection has grown to more than one hundred items covering a broad cross section of legal topics. Blawgs can also be retrieved by keywords or browsed by subject, name, or title.” To access our visualization of the legal blogosphere (pictured above) … please click here.