Tag: artificial intelligence and law
International Conference on Artificial Intelligence and Law (Rome 2013 – Registration is Now Open!)
As a member of the AI+Law 2013 Program Committee it is my pleasure to invite you to attend the International Conference on Artificial Intelligence and Law – Rome 2013 — June 10-14. The conference will feature the core program of peer reviewed papers, research abstracts and project demos. In addition, the conference features two days of workshops and tutorials in topics such as Computational Models of Natural Argument, Textual Extraction from Legal Resources, Machine Learning in E-Discovery, Network Analysis in Law, XML Schemas for Legal Rules, Data Driven Artificial Intelligence in Law, etc.
I hope to see you in Rome this Summer for AI+Law 2013!
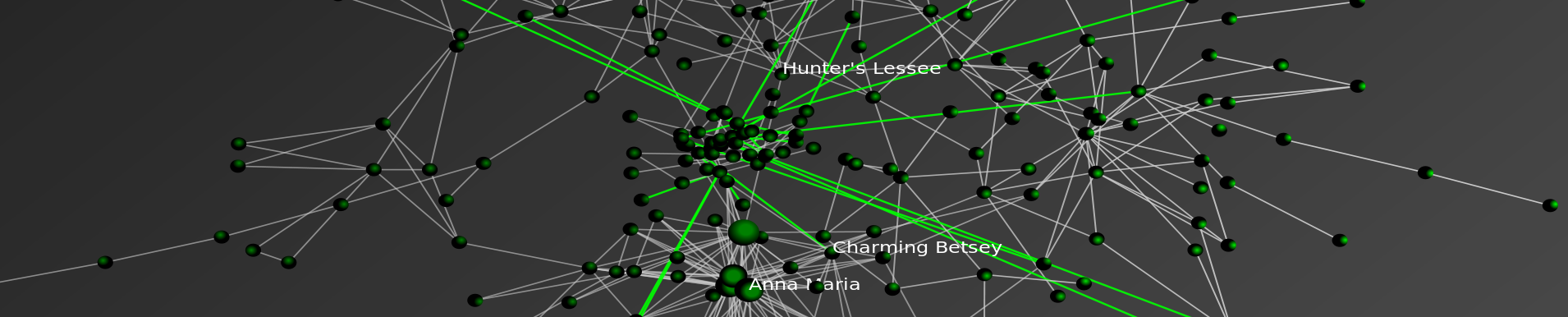
Workshop “Network Analysis in Law” @ International Conference on Artificial Intelligence and Law – Rome 2013
This Workshop builds upon the “Network Analysis and the Law” Tutorial that Mike Bommarito and I ran at Jurix 2011 in Vienna.
It was a great honor to be an organizer for both the overall Artificial Intelligence and Law 2013 Conference as well as the Network Analysis and Law workshop.
Looking forward to great week of rigorous technical papers at Artificial Intelligence and Law 2013 in Rome in early June!
ReInvent Law London 2013 – A Free, Open & Crowd Sourced Conference – June 14, 2013 in Central London
#ReInvent Law London 2013 will be an open, crowd-sourced conference! Talks will be submitted by the public and then those proposals will be voted upon by the public. Anyone can pitch a topic, and everyone can vote.
Here are the rules:
1. Submit your 300-word or 30-second-YouTube-video pitch at www.ReInventLawLondon.com between now and midnight on April 5, 2013.
2. Vote for your favorite pitch when the voting window opens in early April. One person, one vote—but feel free to use Twitter, Facebook and LinkedIn to encourage colleagues, friends, family and more to vote for your pitch.
3. Talks must relate to some aspect of law + technology + innovation + entrepreneurship. This is about big ideas—no sales pitches or product pushing.
4. Winners will have up to 10 minutes to speak, and will then respond to dynamic, real-time, audience-driven Q&A.
5. You can also sign up here for a FREE ticket to witness ReInvent Law London, June 14, 2013. Each of our previous events have sold out – so sign up today!
#ReInventLaw London 2013 is part of Michigan State University College of Law’s 21st Century Law Practice Summer Program.
Learn more about our laboratory and its 4 pillars — { Law + Tech + Design + Delivery }
@ www.ReInventLaw.com
RoundUp of Coverage of ReInvent Law Silicon Valley 2013 – More Events Coming in 2013 and Beyond – Including ReInvent Law London + ReInvent Law New York
This is Hardly a Complete List but These Provide a Good Overview ….
The Future of Law as Seen From Silicon Valley (The AmLaw Daily – Aric Press)
‘Law is Broken.’ Will These Legal Tech Gurus Bring About Change? (ABA Journal – Law Scribbler/Rachel M. Zahorsky)
Thoughts on the Future of Law from ReInvent Law – Silicon Valley 2013 (The Legal Whiteboard – Jerry Organ)
ReInvent Law is a Really Big Deal (The Legal Whiteboard – Bill Henderson)
ReInvent Law Recap: A Speaker’s and Attendee’s Perspective (The Bionic Lawyer – Kevin Colangelo)
Twitter Recap of #ReInventLaw Silicon Valley (Innov8Social)
Five Core Themes of Legal Services Industry Reinvention (Legal 2050 Blog – J.B. Ruhl)
New Perspectives on the Legal Sector (Virtual Intelligence)
Enough Pain?: Time to Reinvent Law (ERM Legal Solutions – Larry Bridgesmith)
Live Blogging from ReInvent Law Silicon Valley 2013 (Prism Legal – Ron Friedmann)
Archived Tweets and Other Resources from #ReInventLaw Silicon Valley 2013 (Legal Informatics Blog – RC Richards)
Couple More Things …
Here is the Conference Website
Here is the Official Schedule of Presentations from March 8, 2013
And Finally More Events Coming in 2013 …
ReInventLaw London – June 14, 2013
ReInvent Law New York – Fall 2013
