Tag: network analysis
Visualizing the East Anglia Climate Research Unit Leaked Email Network
As reported in a wide variety of news outlets, last week, a large amount of data was hacked from the Climate Research Unit at the University of East Anglia. This data included both source code for the CRU climate models, as well as emails from the individuals involved with the group. For those interested in background information, you can read the NY Times coverage here and here. Read the Wall Street Journal here. Read the Telegraph here. For those interested in searching the emails, the NY Times directs the end user to http://www.eastangliaemails.com/.
Given the data is widely available on the internet, we thought it would be interesting to analyze the network of contacts found within these leaked emails. Similar analysis has been offered for large datasets such as the famous Enron email data set. While there may be some selection issues associated with observing this subset of existing emails, we believe this network still gives us a “proxy” into the structure of communication and power in an important group of researchers (both at the individual and organization level).
To build this network, we processed every email in the leaked data. Each email contains a sender and at least one recipient on the To:, Cc:, or Bcc: line. The key assumption is that every email from a sender to a recipient represents a relationship between them. Furthermore, we assume that more emails sent between two people, as a general proposition indicates a stronger relationship between individuals.
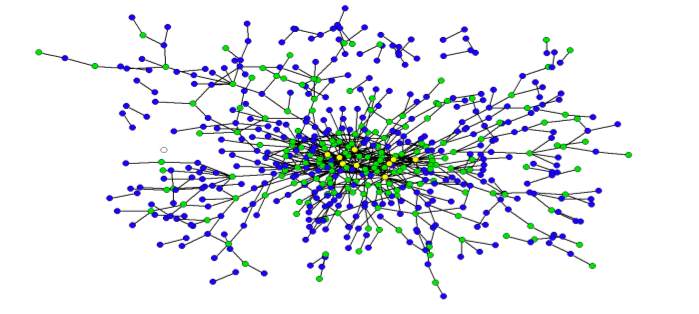
To visualize the network, we draw a blue circle for every email address in the data set. The size of the blue circle represents how many emails they sent or received in the data set – bigger nodes thus sent or received a disproportionate number of emails. Next, we draw grey lines between these circles to represent that emails were sent between the two contacts. These lines are also sized by the number of emails sent between the two nodes.
Typically, we would also provide full labels for nodes in a network. However, we decided to engage in partial “anonymization” for the email addresses of those in the data set. Thus, we have removed all information before the @ sign. For instance, an email such as johndoe@umich.edu is shown as umich.edu in the visual. If you would like to view this network without this partial “anonymization,” it is of course possible to download the data and run the source code provided below.
Note: We have updated the image. Specifically, we substituted a grey background for the full black background in an effort to make the visual easier to read/interpret.
Click here for a zoomable version of the visual on Microsoft Seadragon.
Don’t forget to use SeaDragon’s fullscreen option:
Hubs and Authorities:
In addition to the visual, we provide hub and authority scores for the nodes in the network. We provide names for these nodes but do not provide their email address.
Authority
- Phil Jones: 1.0
- Keith Briffa: 0.86
- Tim Osborn: 0.80
- Jonathan Overpeck: 0.57
- Tom Wigley: 0.54
- Gavin Schmidt: 0.54
- Raymond Bradley: 0.52
- Kevin Trenberth: 0.49
- Benjamin Santer: 0.49
- Michael Mann: 0.46
Hubs returns nearly identical ranks with slightly perturbed orders with the notable exception that the UK Met Office IPCC Working Group has the highest hub score.
Thus, so far as these emails are a reasonable “proxy” for the true structure of this communication network, these are some of the most important individuals in the network.
Source Code:
Unlike some existing CRU code, the code below is documented, handles errors, and is freely available.
“Sink Method” Poster for Conference on Empirical Legal Studies (CELS 2009 @ USC)
 As we mentioned in previous posts, Seadragon is a really cool product. Please note load times may vary depending upon your specific machine configuration as well as the strength of your internet connection. For those not familiar with how to operate it please see below. In our view, the Full Screen is best the way to go ….
As we mentioned in previous posts, Seadragon is a really cool product. Please note load times may vary depending upon your specific machine configuration as well as the strength of your internet connection. For those not familiar with how to operate it please see below. In our view, the Full Screen is best the way to go ….
Programming Dynamic Models in Python-Part 3: Outbreak on a Network
In this post, we will continue building on the basic models we discussed in the first and second tutorials. If you haven’t had a chance to take a look at them yet, definitely go back and at least skim them, since the ideas and code there form the backbone of what we’ll be doing here.
In this tutorial, we will build a model that can simulate outbreaks of disease on a small-world network (although the code can support arbitrary networks). This tutorial represents a shift away from both:
a) the mass-action mixing of the first two and and
b) the assumption of social homogeneity across individuals that allowed us to take some shortcuts to simplify model code and speed execution. Put another way, we’re moving more in the direction of individual-based modeling.
When we’re done, your model should be producing plots that look like this:
Red nodes are individuals who have been infected before the end of the run, blue nodes are never-infected individuals and green ones are the index cases who are infectious at the beginning of the run.
And your model will be putting out interesting and unpredictable results such as these:
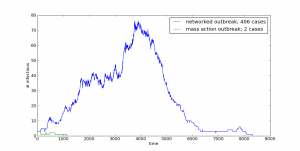
In order to do this one, though, you’re going to need to download and install have igraph for Python on your system.
Individual-Based Networks
It is important to make the subtle distinction between individual and agent based models very clear here. Although the terms are often used interchangeably, referring to our nodes, who have no agency, per se, but are instead fairly static receivers and diffusers of infection, as agents, seems like overreaching. Were they to exhibit some kind of adaptive behavior, i.e., avoiding infectious agents or removing themselves from the population during the infective period, they then become more agent-like.
This is not to under- or over-emphasize the importance or utility of either approach, but just to keep the distinction in mind to avoid the “when all you have is a hammer, everything looks like a nail” problem.
In short, adaptive agents are great, but they’re overkill if you don’t need them for your specific problem.
Small World Networks
The guiding idea behind small-world networks is that they capture some of the structure seen in more realistic contact networks: most contacts are regular in the sense that they are fairly predicable, but there are some contacts that span tightly clustered social groups and bring them together.
In the basic small-world model, an individual is connected to some (small, typically <=8) number of his or her immediate neighbors. Some fraction of these network connections are then randomly re-wired, so that some individuals who were previously distant in network terms – i.e., connected by a large number of jumps – are now adjacent to each other. This also has the effect of shortening the distance between their neighbors and individuals on the other side of the graph. Another way of putting this is that we have shortened the average path length and increased the average reachability of all nodes.
These random connections are sometimes referred to as “weak ties”, as there are fewer of these ties that bridge clusters than there are within clusters. When these networks are considered from a sociological perspective, we often expect to find that the relationship represented by a weak tie is one in which the actors on either end have less in common with each other than they do with their ‘closer’ network neighbors.
Random networks also have the property of having short average path lengths, but they lack the clustering that gives the small-world model that pleasant smell of quasi-realism that makes them an interesting but largely tractable, testing ground for theories about the impact of social structure on dynamic processes.
Installation and Implementation Issues
If you have all the pre-requisites installed on your system, you should be able to just copy and paste this code into a new file and run it with your friendly, local Python interpreter. When you run the model, you should first see a plot of the network, and when you close this, you should see a plot of the number of infections as a function of time shortly thereafter.
Aside from the addition of the network, the major conceptual difference is that the model operates on discrete individuals instead of a homogeneous population of agents. In this case, the only heterogeneity is in the number and identity of each individual’s contacts, but there’s no reason we can’t (and many do) incorporate more heterogeneity (biological, etc.) into a very similar model framework.
With Python, this change in orientation to homogeneous nodes to discrete individuals seems almost trivial, but in other languages it can be somewhat painful. For instance, in C/++, a similar implementation would involve defining a struct with fields for recovery time and individual ID, and defining a custom comparison operator for these structs. Although this is admittedly not a super-high bar to pass, it adds enough complexity that it can scare off novices and frustrate more experienced modelers.
Perhaps more importantly, it often has the effect of convincing programmers that a more heavily object-oriented approach is the way to go, so that each individual is a discrete object. When our individuals are as inert as they are in this model, this ends up being a waste of resources and makes for significantly more cluttered code. The end result can often be a model written in a language that is ostensibly faster than Python, such as C++ or Java, that runs slower than a saner (and more readable) Python implementation.
For those of you who are playing along at home, here are some things to think about and try with this model:
- Change the kind of network topology the model uses (you can find all of the different networks available in igraph here).
- Incorporate another level of agent heterogeneity: Allow agents to have differing levels of infectivity (Easier); Give agents different recovery time distributions (Harder, but not super difficult).
- Make two network models – you can think of them as separate towns – and allow them to weakly influence each other’s outbreaks. (Try to use the object-oriented framework here with minimal changes to the basic model.)
That’s it for tutorial #3, (other than reviewing the comment code which is below) but definitely check back for more on network models!
In future posts, we’ll be thinking about more dynamic networks (i.e., ones where the links can change over time), agents with a little more agency, and tools for generating dynamic visualizations (i.e., movies!) of stochastic processes on networks.
That really covers the bulk of the major conceptual issues. Now let’s work through the implementation.
Click Below to Review the Implementation and Commented Code!
Continue reading “Programming Dynamic Models in Python-Part 3: Outbreak on a Network”
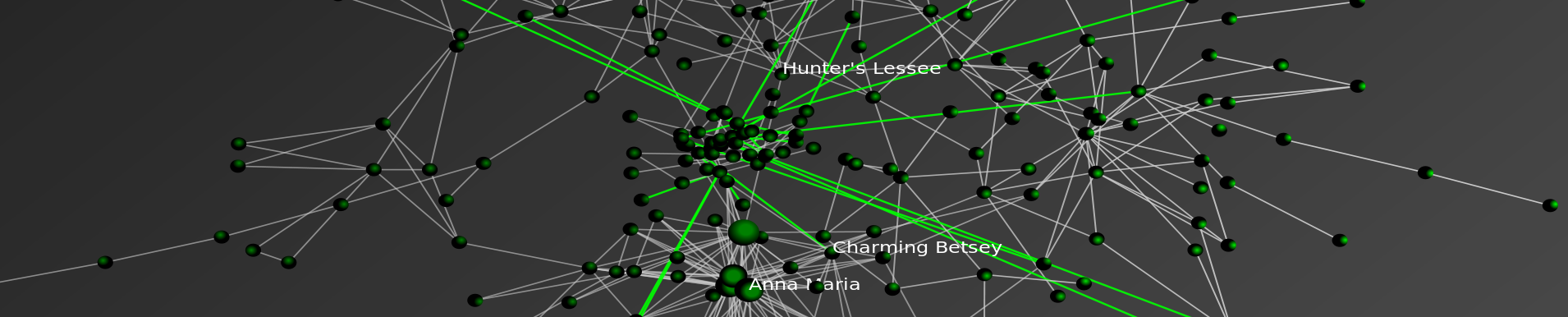
New Paper: Properties of the United States Code Citation Network
We have been working on a larger paper applying many concepts from structural analysis and complexity science to the study of bodies of statutory law such as the United States Code. To preview the broader paper, we’ve published to SSRN and arXiv a shorter, more technical analysis of the properties of the United States Code’s network of citations.
Click here to Download the Paper!
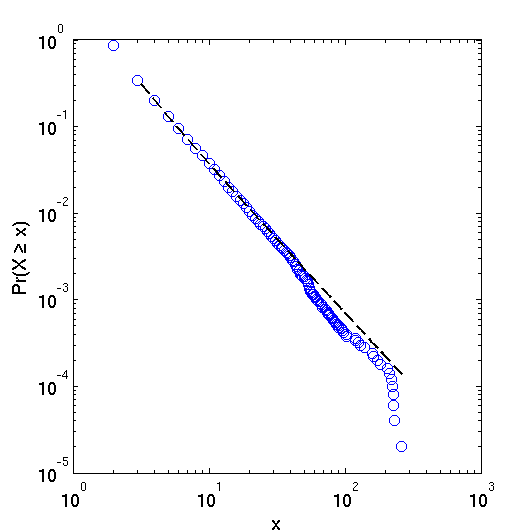
Abstract: The United States Code is a body of documents that collectively comprises the statutory law of the United States. In this short paper, we investigate the properties of the network of citations contained within the Code, most notably its degree distribution. Acknowledging the text contained within each of the Code’s section nodes, we adjust our interpretation of the nodes to control for section length. Though we find a number of interesting properties in these degree distributions, the power law distribution is not an appropriate model for this system.
Hustle and Flow: A Social Network Analysis of the American Federal Judiciary [Repost from 3/25]
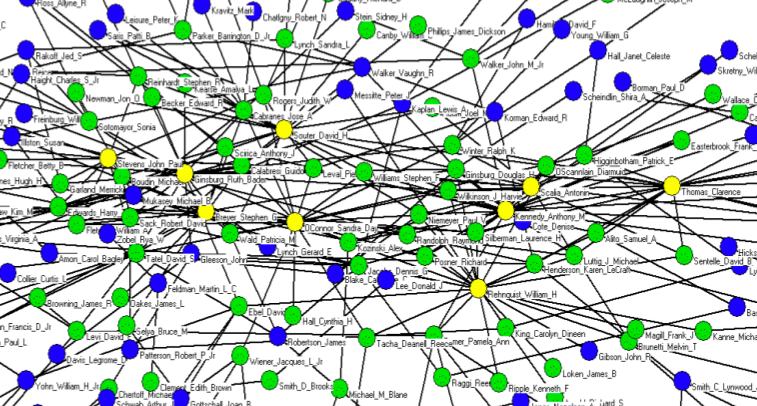
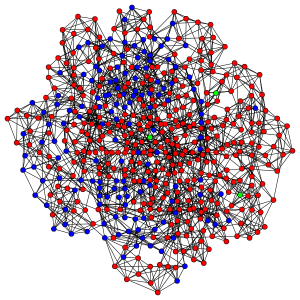
Together with Derek Stafford from the University of Michigan Department of Political Science, Hustle and Flow: A Social Network Analysis of the American Federal Judiciary represents our initial foray into Computational Legal Studies. The full paper contains a number of interesting visualizations where we draw various federal judges together on the basis of their shared law clerks (1995-2004). The screen print above is a zoom very center of the center of the network. Yellow Nodes represent Supreme Court Justices, Green Nodes represent Circuit Court Justices, Blue Nodes represent District Court Justices.
There exist many high quality formal models of judicial decision making including those considering decisions rendered by judges in judicial hierarchy, whistle blowing, etc. One component which might meaningfully contribute to the extent literature is the rigorous consideration of the social and professional relationships between jurists and the impacts (if any) these relationships impose upon outcomes. Indeed, from a modeling standpoint, we believe the “judicial game” is a game on a graph–one where an individual strategic jurist must take stock of time evolving social topology upon which he or she is operating. Even among judges of equal institutional rank, we observe jurists with widely variant levels social authority (specifically social authority follows a power law distribution).
So what does all of this mean? Take whistle blowing — the power law distribution implies that if the average judge has a whistle, the “super-judges” we identify within the paper could be said to have an air horn. With the goal of enriching positive political theory / formal modeling of the courts, we believe the development of a positive theory of judicial social structure can enrich our understanding of the dynamics of prestige and influence. In addition, we believe, at least in part, “judicial peer effects” can help legal doctrine socially spread across the network. In that vein, here is a view of our operationalization of the social landscape … a wide shot of the broader network visualized using the Kamada-Kawai visualization algorithm:
Here is the current abstract for the paper: Scholars have long asserted that social structure is an important feature of a variety of societal institutions. As part of a larger effort to develop a fully integrated model of judicial decision making, we argue that social structure-operationalized as the professional and social connections between judicial actors-partially directs outcomes in the hierarchical federal judiciary. Since different social structures impose dissimilar consequences upon outputs, the precursor to evaluating the doctrinal consequences that a given social structure imposes is a descriptive effort to characterize its properties. Given the difficulty associated with obtaining appropriate data for federal judges, it is necessary to rely upon a proxy measure to paint a picture of the social landscape. In the aggregate, we believe the flow of law clerks reflects a reasonable proxy for social and professional linkages between jurists. Having collected available information for all federal judicial law clerks employed by an Article III judge during the “natural” Rehnquist Court (1995-2004), we use these roughly 19,000 clerk events to craft a series of network based visualizations. Using network analysis, our visualizations and subsequent analytics provide insight into the path of peer effects in the federal judiciary. For example, we find the distribution of “degrees” is highly skewed implying the social structure is dictated by a small number of socially prominent actors. Using a variety of centrality measures, we identify these socially prominent jurists. Next, we draw from the extant complexity literature and offer a possible generative process responsible for producing such inequality in social authority. While the complete adjudication of a generative process is beyond the scope of this article, our results contribute to a growing literature documenting the highly-skewed distribution of authority across the common law and its constitutive institutions.
Programming Dynamic Models in Python: Coding Efficient Dynamic Models
 In the next few tutorials, we’re going to transition to exploring how to model dynamics on a network.
In the next few tutorials, we’re going to transition to exploring how to model dynamics on a network.
The first tutorial was a bit of a blockbuster length-wise because there was a lot of ground to cover to get the basic model up and running. Moving forward, we’ll be able to go a bit more incrementally, adding elements to the basic model as we go. If you don’t feel comfortable with the original, go back and take a look at it and make sure that it makes sense to you before moving on.
We’re first going to deal with some of the efficiency issues in the first model. After this, we’ll make some basic changes to the architecture of the SIR program that makes it more amenable to contact patterns on a social network.
Finally, we’ll show you how to how to take the output of your epidemic model and generate animations like this one:
Blue nodes are exposed but uninfected, red nodes are infectious, and yellow ones have recovered.
The movie is a bit of a carrot to get you through the less flashy, but, I promise, important and actually interesting nuts and bolts of putting these kinds of models together.
This tutorial is going to cover the last two big things that we need to tackle before we get to the model of an outbreak on a network. So, here we go!
New Concepts
1. Arbitrarily Distributed Infectious Periods
First, we’re going to deal with the duration of the infectious period. The assumption of an exponentially distributed infectious period is unnecessarily restrictive for a general model of diffusion, and the way the original code goes about recovering individuals – drawing a random number on every step for every infectious individual – should strike you as both inelegant and computationally inefficient, particularly when the rate of recovery is slow and there are many infectious individuals.
In order to deal with this, we’re going to introduce two new tools. The first is the scipy.stats toolkit and the second is a neat (and very easy to use) data structure called a heap.
A heap is in very many ways what it sounds like: imagine a pile of trash in a landfill; the tires and rusting washing machines are on the bottom, while the pop cans and grocery store receipts are closer to the top.
As a programming tool, a heap is useful because it always keeps the smallest (or largest, depending on your preference) item at the top of the list. It also allows for linear-time insertion and removal of objects. This means that the time it takes to execute an action grows proportionally to the size of the list, so if it has N items, it takes N*C steps (where C is a constant) to process the list, and if it has 2*N items, it takes 2*N*C steps. Other ways of sorting could take N^2 or worse steps to do the same.
In our outbreak model, the top item on the heap is always going to be the time at which the next individual recovers. By doing this, we can avoid the loop in the first tutorial (and replicated in one implementation here) that checks whether each infectious individual is going to recover on each step.
Looping over everyone is the most intuitive way to check if they’re going to recover, but it’s very inefficient, especially when infectious periods are long and the population is large. It’s also problematic from a theoretical perspective, because it chains us to exponentially distributed recovery periods.
Exponentially distributed infectious periods make analytic sense for a deterministic model, but your disease or *insert diffusible here* may have a constant or normally distributed ‘infectious’ period.
By using a heap-based implementation, as you will see, we can use arbitrary recovery periods, and Python’s implementation of the heap is very straightforward – just a small twist on the usual list using the heapq module.
2. Object Oriented Programming
One of Python’s strengths is that it supports a style of programming that mixes the best of object-oriented programming (OOP) and procedural or imperative programming.
We won’t go too deep into the details of OOP here, but the real strength of OOP implementations are that they allow code to be easily re-used in other programs (Python’s all-powerful ‘import‘ statement really makes this true) and also forces some structure on what functions have access to what variables, etc.
Click Below to Review the Implementation and Commented Code!
Continue reading “Programming Dynamic Models in Python: Coding Efficient Dynamic Models”
Programming Dynamic Models in Python
 In this series of tutorials, we are going to focus on the theory and implementation of transmission models in some kind of population.
In this series of tutorials, we are going to focus on the theory and implementation of transmission models in some kind of population.
In epidemiology, it is common to model the transmission of a pathogen from one person to another. In the social sciences and law, we may be interested in thinking about the way in which individuals influence each other’s opinions, ideology and actions.
These two examples are different, but in many ways analogous: it is not difficult to imagine the influence that one individual has on another as being similar to the infectivity of a virus in the sense that both have the ability to change the state of an individual. One may go from being susceptible to being infected, or from unconvinced to convinced.
Additionally, social networks have become an important area of study for epidemiological modelers. We can imagine that the nature of the network is different than the ones we think about in the social sciences: when studying outbreaks of a sexually transmitted disease, one doesn’t care all that much about the friendship networks of the people involved, while this would be very important for understanding the impact of social influence on depression and anxiety.
As someone who spends a lot of time working in the space where epidemiology and sociology overlap, I end up thinking a lot about these models – and their potential application to new and different problems and am really excited to share them with a broader audience here. In this first tutorial, I’m going to introduce a simple Susceptible-Infected-Recovered (SIR) model from infectious disease epidemiology and show a simple, Pythonic implementation of it. We’ll work through the process of writing and optimizing this kind of model in Python and, in the final tutorials, will cover how to include a social network in the simulation model.
In order to use the example below, all you need to have installed is a current version of Python (2.4+ is probably best) and the excellent Python plotting package Matplotlib in order to view output. If you don’t have Matplotlib and don’t want to go and install it (although I guarantee you won’t regret it), just comment out import for Pylab and any lines related to plotting.
Model Assumptions
1. State Space / Markov Model
Before getting into the mechanics of the model, let’s talk about the theory and assumptions behind the model as it is implemented here:
The SIR model is an example of a ‘state space‘ model, and the version we’ll be talking about here is a discrete time, stochastic implementation that has the Markov property, which is to say that its state at time t+1 is only conditional on the parameters of the model and its state at time t.
For the uninitiated, in a state-space model, we imagine that each individual in the system can only be in one state at a time and transitions from state to state as a function of the model parameters, i.e., the infectivity of the pathogen or idea and the rate of recovery from infection…and the other states of the system. In other words, the system has endogenous dynamics. This is what makes it both interesting and in some ways difficult to work with.
In the SIR model, we assume that each infectious individual infects each susceptible individual at rate beta. So, if beta = .5, there is a 50% chance that each susceptible individual will be infected by an exposure to an infectious individual. For this reason, as the number of infected individuals in the system grows, the rate at which the remaining susceptible individuals is infected also grows until the pool of susceptible individuals is depleted and the epidemic dies out.
The other parameter we care about is gamma, or the rate of recovery. If gamma is also equal to .5, we assume that the average individual has a 50% chance of recovering on a given day, and the average duration of infectiousness will be 1/gamma, or 2 days.
We refer to the ratio beta/gamma as the basic reproductive ratio, or Ro (‘R naught’). When this number is less than one, we typically expect outbreaks to die out quickly. When this quantity is greater than one, we expect that the epidemic will grow and potentially saturate the whole population.
2. Homogeneous Mixing:
We’re assuming a world in which everyone has simultaneous contact with everyone else. In other words, we’re thinking of a totally connected social network. If you’re a regular reader of this blog, a social network enthusiast, or in some other way a thinking person, this assumption probably seems unreasonable. It turns out, however, that for many diseases, this assumption of homogeneous or ‘mass-action’ mixing, which was actually originally borrowed from chemistry, turns out to be a reasonable approximation.
For instance, if we are trying to approximate the transmission dynamics of a very infectious pathogen like measles in a city or town, we can usually overlook social network effects at this scale and obtain a very good fit to the data. This is because even very weak contacts can transmit measles, so that friendships and other types of close contacts are not good predictors of risk. Instead, we we are better off looking at a higher level of organization – the pattern of connection between towns and cities to understand outbreaks. In a social context, something like panic may be thought of as being super-infectious (for a really interesting study about the potential relationship between social panic and flu dynamics, see this paper by Josh Epstein).
This is, however, a generally problematic assumption for most problems of social influence, but an understanding of this most basic version of the model is necessary to move on to more complicated contact patterns.
3. Exponentially distributed infectious periods:
In the most basic implementation of the SIR model, we assume that each infectious individual has some probability of recovering on every step. If our model steps forwards in days and individuals have a .5 probability of recovery on each day, we should expect that the time to recovery follows an exponential distribution. This means that most people will be pretty close to the mean, but some will take a relatively long time to recover. This is accurate for a lot of cases, but definitely not for all. In some diseases, recovery times may be lognormal, power-law or bimodally disributed. For social models, the notion of an ‘infectious period’ may not make a tremendous amount of sense at all. But it allows for a very simple and transparent implementation, so we’ll use it here.
CLICK THROUGH TO SEE THE IMPLEMENTATION and RELEVANT PYTHON CODE!
Algorithmic Community Detection in Networks
Community detection in networks is an extremely important part of the broader network science literature. For quite a while, we have meant to highlight the extremely useful review article written by Mason Porter (Oxford) Jukka-Pekka Onnela (Harvard/Oxford) and Peter J Mucha (UNC). Rather than offer our description of the article, we thought it best to highlight commentary on the subject provided by the authors.
For example, in describing the paper over at Harvard’s Complexity and Social Networks Blog Jukka-Pekka Onnela posted the following… “Uncovering the “community” structure of social networks has a long history, but communities play a pivotal role in almost all networks across disciplines. Intuitively, one can think of a network community as consisting of a group of nodes that are relatively densely connected to each other but sparsely connected to other dense groups of nodes. Communities are important because they are thought to have a strong bearing on functional units in many networks. So, for example, communities in social networks can correspond to different social groups, such as family, whereas web pages dealing with a given subject tend to form topical communities. The concept is simple enough, but it turns out that coming up with precise mathematical definitions and algorithms for community detection is one of the most challenging problems in network science. Recently, a lot of the research in this area has been done using ideas from statistical physics, which has an arsenal of tools and concepts to tackle the problem. Unfortunately (but understandably) relatively few non-physicists like to read statistical physics papers.”
These scholars quote Mark Newman noting “[T]he development of methods for finding communities within networks is a thriving sub-area of the field, with an enormous number of different techniques under development. Methods for understanding what the communities mean after you find them are, by contrast, still quite primitive, and much needs to be done if we are to gain real knowledge from the output of our computer programs.” They later note “the problem of how to validate and use communities once they are identified is almost completely open.”
Anyway, if you are interested in learning more about this important piece of the network science toolkit … we suggest you read this paper!
Christakis and Fowler in Wired Magazine
Today marks the official release of Connected: The Surprising Power of Our Social Networks and How They Shape Our Lives by Nicholas A. Christakis & James H. Fowler. There has been some really good publicity for the book including the cover story in last Sunday’s New York Times Magazine. However, given the crisp visualizations — my favorite is the above article from Wired Magazine. Click on the visual above to read the article!