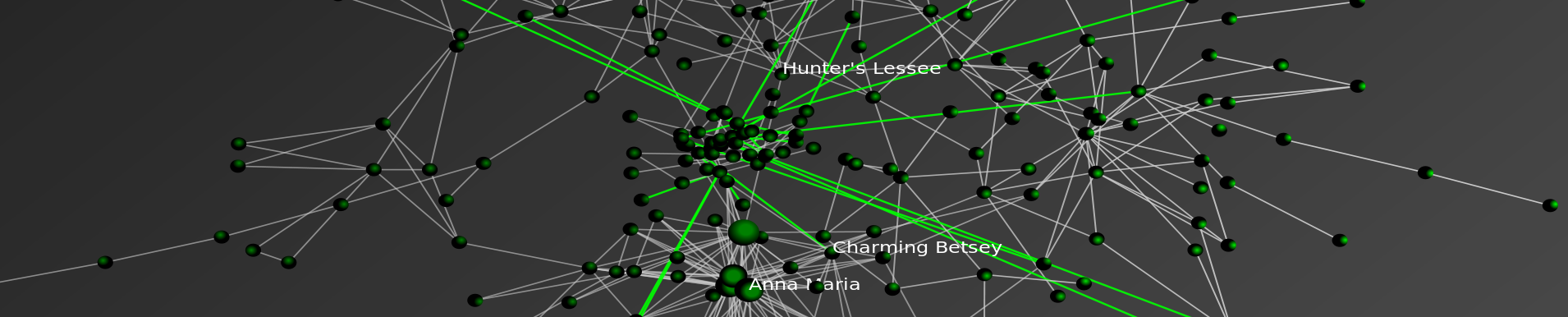
Tag: network analysis
Modeling the Financial Crisis [ From Nature ]
This week’s issue of Nature offers two brief but meaningful articles on the financial crisis. Here are the abstracts:
Financial Systems: Ecology and Economics (By Neil Johnson & Thomas Lux): “In the run-up to the recent financial crisis, an increasingly elaborate set of financial instruments emerged, intended to optimize returns to individual institutions with seemingly minimal risk. Essentially no attention was given to their possible effects on the stability of the system as a whole. Drawing analogies with the dynamics of ecological food webs and with networks within which infectious diseases spread, we explore the interplay between complexity and stability in deliberately simplified models of financial networks. We suggest some policy lessons that can be drawn from such models, with the explicit aim of minimizing systemic risk.”
Systemic Risk in Banking Ecosystems (By Andrew G. Haldane & Robert M. May): “In the run-up to the recent financial crisis, an increasingly elaborate set of financial instruments emerged, intended to optimize returns to individual institutions with seemingly minimal risk. Essentially no attention was given to their possible effects on the stability of the system as a whole. Drawing analogies with the dynamics of ecological food webs and with networks within which infectious diseases spread, we explore the interplay between complexity and stability in deliberately simplified models of financial networks. We suggest some policy lessons that can be drawn from such models, with the explicit aim of minimizing systemic risk.”
Introduction to Computing for Complex Systems — ICPSR 2010 — My Full Course Slides Available Online!
I am going to bump this post to front of the blog one last time as there has been some interest in this material. It has now been several weeks since we completed the full four week class here at the ICPSR Program in Quantitative Methods. In this course, I (together with my colleagues) highlight the methods of complex systems as well as several environments designed to explore the field. These include Netlogo (agent based models and network models), Vensim (system dynamics / ecological modeling) and Pajek (empirical network analysis). In the final week, we cover a variety of advanced topics:
- (a) Community Detection in Networks
- (b) Computational Linguistics / Natural Language Processing
- (c) Diffusion Models and Mathematical Modeling with Data
- (d) Exponential Random Graph (p*) Models
- (e) Information Retrieval / Webscraping
Although, we do not work with more advanced languages within the course, those who need to conduct complex analysis are directed to alternatives such as R, Python, Java, etc.
Anyway, the slides are designed to be fully self-contained and thus allow for individually paced study of the relevant material. If you work through the slides carefully you should be able to learn the software as well as many of the core principles associated with the science of complex systems. The material should be available online indefinitely. If you have questions, feel free to email me.
The Architecture of the Brain — Network or Hierarchy ? [BBC News & PNAS ]
This week in the Proceedings of the National Academy of Sciences comes a very important article entitled Hypothesis-driven structural connectivity analysis supports network over hierarchical model of brain architecture by Richard H. Thompson and Larry W. Swanson of the University of Southern California. Above is the BBC coverage regarding the paper. Here is the press release from USC. Here is the story from Science Daily. This article is worth the read!
ICPSR 2010 Summer Program — Introduction to Computing for the Study of Complex Systems
This summer I will be teaching a summer course entitled Introduction to Computing for the Study of Complex Systems at the ICPSR Summer Program in Quantitative Methods. For those not familiar, ICSPR has been offering summer classes in methods since 1963. The Summer Program current features dozens of courses including basic and advanced econometrics, bayesian statistics, game theory, complex systems, network analysis, quantitative analysis of crime, etc.
The Complex Systems Computing Module runs together with the Complex Systems lectures offered by Ken Kollman (Michigan), Scott E. Page (Michigan), P.J. Lamberson (MIT-Sloan) and Kate Anderson (Carnegie Mellon). Here is the syllabus for the lecture.
The first computing session is tonight from 6-8pm at the ICPSR Computer Lab. If you click here or click on the image above you will be taken to a dedicated page that will host the syllabus and course slides! Note: The slides and assignments will not be posted until the conclusion of each class.
Harambeenet 2010 @ Duke Computer Science Department
Today — Mike, Jon and I are at the 2010 Harambeenet Conference here in the Duke Computer Science Department. The conference is centered upon network science and computer science education. It features lots of interdisciplinary scholarship and applications of computer science techniques in novel domains. We are looking forward to an interesting couple of days of discussion!
“A Taxonomy of Networks” New Paper on the Physics arXiv
An exciting new paper entitled “A Taxonomy of Networks” by Jukka-Pekka Onnela, Daniel J. Fenn, Stephen Reid, Mason A. Porter, Peter J. Mucha, Mark D. Fricker & Nick S. Jones just hit the Physics arXiv. I wanted to flag it for anyone who might be interested.
Here is the abstract: “The study of networks has grown into a substantial interdisciplinary endeavor across the natural, social, and information sciences. Yet there have been very few attempts to investigate the interrelatedness of the different classes of networks studied by different disciplines. Here, we introduced a framework to establish a taxonomy of networks from various origins. The provision of this family tree not only helps understand the kinship of networks, but also facilitates the transfer of empirical analysis, theoretical modeling, and conceptual developments across disciplinary boundaries. The framework is based on probing the mesoscopic properties of networks, an important source of heterogeneity for their structure and function. Using our method, we computed a taxonomy for 752 individual networks and a separate taxonomy for 12 network classes. We also computed three within-class taxonomies for political, fungal, and financial networks, and found them to be insightful in each case.”
Sunbelt Social Networks Conference 2010 – Riva Del Garda
Next week Mike and I will be in Italy for Sunbelt 2010 in Riva Del Garda. Sunbelt features scholars from across the social and physical sciences — Mathematical Sociology, Political Science, Economics, Organization Studies as well as Physics and Applied Math. For those of you attending, we looking forward to seeing you in Italy!
Community Structure in Time-Dependent, Multiscale and Multiplex Networks [ Via Science ]
This morning I participated in the first set panels at the Duke Political Networks Conference. Our panel was entitled “Dynamic Networks.” On the panel was Peter Mucha from UNC-Math, who presented Community Structure in Time-Dependent, Multiscale, and Multiplex Networks [Mucha, Richardson, Macon, Porter, Onnela].
Suffice to say, this is a very exciting paper. Indeed, the paper is in this week’s edition of Science Magazine. The article fills an important hole in the broader literature and I believe the approach outlined therein will be adopted by many scholars.
Here is the abstract: “Network science is an interdisciplinary endeavor, with methods and applications drawn from across the natural, social, and information sciences. A prominent problem in network science is the algorithmic detection of tightly connected groups of nodes known as communities. We developed a generalized framework of network quality functions that allowed us to study the community structure of arbitrary multislice networks, which are combinations of individual networks coupled through links that connect each node in one network slice to itself in other slices. This framework allows studies of community structure in a general setting encompassing networks that evolve over time, have multiple types of links (multiplexity), and have multiple scales.”
Nicholas Christakis: The Hidden Influence of Social Networks [ Ted 2010 ]
If this does not load please click here to access the TED page.