
< Access the Article Here >
 Mike and I had the great pleasure of spending several years at the University of Michigan Center for the Study of Complex Systems where John Holland spent a fair amount of his time. He was a very giving person and of course – a true genius! Rest in peace.
Mike and I had the great pleasure of spending several years at the University of Michigan Center for the Study of Complex Systems where John Holland spent a fair amount of his time. He was a very giving person and of course – a true genius! Rest in peace.
From the story in Vox … “Surprisingly, just letting people get on the plane in an order unrelated to their seats leads to slightly faster boarding times than the standard method.”
 As a member of the AI+Law 2013 Program Committee it is my pleasure to invite you to attend the International Conference on Artificial Intelligence and Law – Rome 2013 — June 10-14. The conference will feature the core program of peer reviewed papers, research abstracts and project demos. In addition, the conference features two days of workshops and tutorials in topics such as Computational Models of Natural Argument, Textual Extraction from Legal Resources, Machine Learning in E-Discovery, Network Analysis in Law, XML Schemas for Legal Rules, Data Driven Artificial Intelligence in Law, etc.
As a member of the AI+Law 2013 Program Committee it is my pleasure to invite you to attend the International Conference on Artificial Intelligence and Law – Rome 2013 — June 10-14. The conference will feature the core program of peer reviewed papers, research abstracts and project demos. In addition, the conference features two days of workshops and tutorials in topics such as Computational Models of Natural Argument, Textual Extraction from Legal Resources, Machine Learning in E-Discovery, Network Analysis in Law, XML Schemas for Legal Rules, Data Driven Artificial Intelligence in Law, etc.
I hope to see you in Rome this Summer for AI+Law 2013!

We cover the topic of Swarms at great length in the “Complex Systems in the Social Sciences Course” that I co-teach at the University of Michigan ICPSR Summer Program in Quantitative Methods. If you are interested in learning more here are some of the slides from last year. The 2013 Edition of the Course Begins in July in Ann Arbor!
Starting in the January 2012, Scott E. Page (one of my PhD thesis advisors) will teach Model Thinking (a free online course offered via the consortium that brought you AI Class, Machine Learning, etc.)
Scott and I have previously teamed up to teach Complex Systems @ the ICPSR Summer Methods Program (where I teach the model implementation lab). Over 7,000 people and counting have are already signed up …
I am going to bump this post to front of the blog one last time as there has been some interest in this material. It has now been several weeks since we completed the full four week class here at the ICPSR Program in Quantitative Methods. In this course, I (together with my colleagues) highlight the methods of complex systems as well as several environments designed to explore the field. These include Netlogo (agent based models and network models), Vensim (system dynamics / ecological modeling) and Pajek (empirical network analysis). In the final week, we cover a variety of advanced topics:
Although, we do not work with more advanced languages within the course, those who need to conduct complex analysis are directed to alternatives such as R, Python, Java, etc.
Anyway, the slides are designed to be fully self-contained and thus allow for individually paced study of the relevant material. If you work through the slides carefully you should be able to learn the software as well as many of the core principles associated with the science of complex systems. The material should be available online indefinitely. If you have questions, feel free to email me.
This week’s issue of the Economist has an interesting article entitled Riders on a Swarm. Among other things, the article discusses how attempts to computationally model ant, bee and bird behavior have offered insight into major problems in artificial intelligence.
For those not familiar, the examples discussed within the article are classic models in the science of complex systems. For example, here is the Netlogo implementation of bird flocking. It will run in your browser but requires Java 4.1 or higher. If you decide to take a look — please click setup – then go to make the model run. Once inside the Netlogo GUI, you can explore how various parameter configurations impact the model’s outcomes.
One of the major insights of the bird flocking model is how random starting conditions and local behavioral rules can lead to the emergence of observed behavioral patterns that appear (at least on first glance) to be orchestrated by some sort of top down command structure.
This is, of course, not the case. The model is bottom up and not top down. Both the simplicity and the bottom up flavor of the model are apparent when you explore the model’s code. For those interested, I will take a second and plug the slides from my ICPSR class. In the class, I dedicated about an hour of class time to bird flocking model. Click here for the slides. In the slides, I walk through some of the important features of the code (discussion starts on slide 16).
This week’s “economic focus” in the Economist highlights Agent Based Modeling as an alternative to traditional economic models and methods. As I am currently teaching Agent Based approaches to modeling as part of the ICPSR Introduction to Computing for Complex Systems, I am quite pleased to see this coverage. Indeed, the timing could not be better and I plan to highlight this article in the course!
Here are some highlights from the article: “… Agent-based modelling does not assume that the economy can achieve a settled equilibrium. No order or design is imposed on the economy from the top down. Unlike many models, ABMs are not populated with “representative agents”: identical traders, firms or households whose individual behaviour mirrors the economy as a whole. Rather, an ABM uses a bottom-up approach which assigns particular behavioural rules to each agent. For example, some may believe that prices reflect fundamentals whereas others may rely on empirical observations of past price trends. Crucially, agents’ behaviour may be determined (and altered) by direct interactions between them, whereas in conventional models interaction happens only indirectly through pricing. This feature of ABMs enables, for example, the copycat behaviour that leads to “herding” among investors. The agents may learn from experience or switch their strategies according to majority opinion. They can aggregate into institutional structures such as banks and firms …” For those who are interested, I have made similar points in the post “Complex Models for Dynamic Time Evolving Landscapes –or– Herb Gintis Offers a Strong Rebuke of “Meltdown.“

The State of the Union often provides for dramatic political theatre. While watching President Obama’s first State of the Union Address last night, I could not help but think about a particular subplot associated with the speech–the Republican caucus and the “standing ovation problem.” With respect to being the party not currently occupying the White House–from the individual member all the way up to the full caucus–it is difficult for the individual member to determine (1) whether to applaud (2) if a given statement by the President is worthy of a standing ovation. From my passive consumption of the television coverage, there was clearly significant variation in the number of Republican caucus members standing at any given applause moment.
For those not familiar, here is a State of the Union based description of the standing ovation problem. “The standing ovation model illustrates a familiar decision-making problem: after hearing a given statement by the President a subset of the audience begins to applaud. The applause builds and a few members of the respective caucus may decide to stand up in enthusiastic recognition. In this situation every other member of the respective caucus must decide whether to join the standing individuals in their ovation, or else remain seated. It is not a trivial decision; imagine, for example, that you initially decide to stay down quietly but then find yourself surrounded by people standing and clapping vigorously. It seems plausible that you may feel awkward, change your mind and end up standing up, saving yourself a significant dose of potential embarrassment. Analogously, you probably wouldn’t enjoy being the only person standing and clapping alone in the middle of a crowded chamber of seated people.”
While often considered along with other related information cascade problems, generating agent based models for the so called “standing ovation problem” has been the focus of a number of scholars. For example, along with John Miller (Carnegie Mellon), Michigan CSCS Director Scott E. Page has authored a leading article on the “standing ovation problem.” Using an agent based modeling approach, Miller & Page analyze a variety dynamics associated with this rich problem. For those interested, here is a link to a standing ovation ABM in Netlogo (requires Java).
In this post, we will continue building on the basic models we discussed in the first and second tutorials. If you haven’t had a chance to take a look at them yet, definitely go back and at least skim them, since the ideas and code there form the backbone of what we’ll be doing here.
In this tutorial, we will build a model that can simulate outbreaks of disease on a small-world network (although the code can support arbitrary networks). This tutorial represents a shift away from both:
a) the mass-action mixing of the first two and and
b) the assumption of social homogeneity across individuals that allowed us to take some shortcuts to simplify model code and speed execution. Put another way, we’re moving more in the direction of individual-based modeling.
When we’re done, your model should be producing plots that look like this:
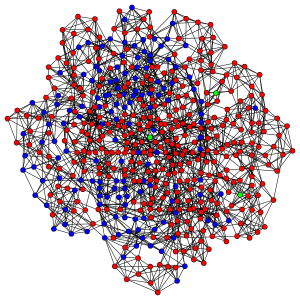
Red nodes are individuals who have been infected before the end of the run, blue nodes are never-infected individuals and green ones are the index cases who are infectious at the beginning of the run.
And your model will be putting out interesting and unpredictable results such as these:
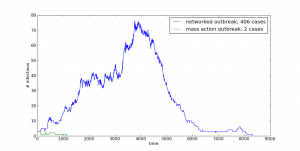
In order to do this one, though, you’re going to need to download and install have igraph for Python on your system.
It is important to make the subtle distinction between individual and agent based models very clear here. Although the terms are often used interchangeably, referring to our nodes, who have no agency, per se, but are instead fairly static receivers and diffusers of infection, as agents, seems like overreaching. Were they to exhibit some kind of adaptive behavior, i.e., avoiding infectious agents or removing themselves from the population during the infective period, they then become more agent-like.
This is not to under- or over-emphasize the importance or utility of either approach, but just to keep the distinction in mind to avoid the “when all you have is a hammer, everything looks like a nail” problem.
In short, adaptive agents are great, but they’re overkill if you don’t need them for your specific problem.
The guiding idea behind small-world networks is that they capture some of the structure seen in more realistic contact networks: most contacts are regular in the sense that they are fairly predicable, but there are some contacts that span tightly clustered social groups and bring them together.
In the basic small-world model, an individual is connected to some (small, typically <=8) number of his or her immediate neighbors. Some fraction of these network connections are then randomly re-wired, so that some individuals who were previously distant in network terms – i.e., connected by a large number of jumps – are now adjacent to each other. This also has the effect of shortening the distance between their neighbors and individuals on the other side of the graph. Another way of putting this is that we have shortened the average path length and increased the average reachability of all nodes.
These random connections are sometimes referred to as “weak ties”, as there are fewer of these ties that bridge clusters than there are within clusters. When these networks are considered from a sociological perspective, we often expect to find that the relationship represented by a weak tie is one in which the actors on either end have less in common with each other than they do with their ‘closer’ network neighbors.
Random networks also have the property of having short average path lengths, but they lack the clustering that gives the small-world model that pleasant smell of quasi-realism that makes them an interesting but largely tractable, testing ground for theories about the impact of social structure on dynamic processes.
If you have all the pre-requisites installed on your system, you should be able to just copy and paste this code into a new file and run it with your friendly, local Python interpreter. When you run the model, you should first see a plot of the network, and when you close this, you should see a plot of the number of infections as a function of time shortly thereafter.
Aside from the addition of the network, the major conceptual difference is that the model operates on discrete individuals instead of a homogeneous population of agents. In this case, the only heterogeneity is in the number and identity of each individual’s contacts, but there’s no reason we can’t (and many do) incorporate more heterogeneity (biological, etc.) into a very similar model framework.
With Python, this change in orientation to homogeneous nodes to discrete individuals seems almost trivial, but in other languages it can be somewhat painful. For instance, in C/++, a similar implementation would involve defining a struct with fields for recovery time and individual ID, and defining a custom comparison operator for these structs. Although this is admittedly not a super-high bar to pass, it adds enough complexity that it can scare off novices and frustrate more experienced modelers.
Perhaps more importantly, it often has the effect of convincing programmers that a more heavily object-oriented approach is the way to go, so that each individual is a discrete object. When our individuals are as inert as they are in this model, this ends up being a waste of resources and makes for significantly more cluttered code. The end result can often be a model written in a language that is ostensibly faster than Python, such as C++ or Java, that runs slower than a saner (and more readable) Python implementation.
For those of you who are playing along at home, here are some things to think about and try with this model:
That’s it for tutorial #3, (other than reviewing the comment code which is below) but definitely check back for more on network models!
In future posts, we’ll be thinking about more dynamic networks (i.e., ones where the links can change over time), agents with a little more agency, and tools for generating dynamic visualizations (i.e., movies!) of stochastic processes on networks.
That really covers the bulk of the major conceptual issues. Now let’s work through the implementation.
Continue reading “Programming Dynamic Models in Python-Part 3: Outbreak on a Network”
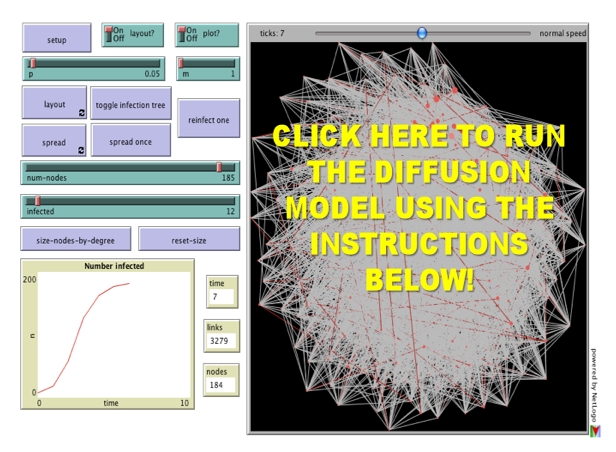 For the third installment of posts related to Reproduction of Hierarchy? A Social Network Analysis of the American Law Professoriate, we offer a Netlogo simulation of intellectual diffusion on the network we previously visualized. As noted in prior posts, we are interested legal socialization and its role in considering the spread of particular intellectual or doctrinal paradigms. This model captures a discrete run of the social epidemiological model we offer in the paper. As we noted within the paper, this represents a first cut on the question—where we favor parsimony over complexity. In reality, there obviously exist far more dynamics than we engage herein. The purpose of this exercise is simply to begin to engage the question. In our estimation, a positive theory of law should engage the sociology of the academy — a group who collectively socialize nearly every lawyer and judge in the United States. In the paper and in the model documentation, we offer some possible model extensions which could be considered in future scholarship.
For the third installment of posts related to Reproduction of Hierarchy? A Social Network Analysis of the American Law Professoriate, we offer a Netlogo simulation of intellectual diffusion on the network we previously visualized. As noted in prior posts, we are interested legal socialization and its role in considering the spread of particular intellectual or doctrinal paradigms. This model captures a discrete run of the social epidemiological model we offer in the paper. As we noted within the paper, this represents a first cut on the question—where we favor parsimony over complexity. In reality, there obviously exist far more dynamics than we engage herein. The purpose of this exercise is simply to begin to engage the question. In our estimation, a positive theory of law should engage the sociology of the academy — a group who collectively socialize nearly every lawyer and judge in the United States. In the paper and in the model documentation, we offer some possible model extensions which could be considered in future scholarship.
Once you click through to the model, here is how it works:
(1) Click the Setup Button in the Upper Left Corner. This will Display the Network in the Circular Layout.
(2) Click the Layout Button. Depending upon the speed of your machine this may take up to 30 seconds. Stop the Layout Button by Re-Clicking the Button.
(3) Click the Size Nodes by Degree Button. You Will Notice the Fairly Central Node Colored in Red. This is School #12 Northwestern University Law School. Observe how we have set the default infected school as #12 Northwestern (Hat Tip to Uri Wilensky). A Full List of School Number is available at the bottom of the page when you click through.
(4) Now, we are ready to begin. Click the Spread Once Button. The idea then reaches its neighbors with probability p (set as a default at .05). You can click the Toggle Infection Tree button (at any point) to observe the discrete paths traversed by the idea.
(5) Click the Spread Once Button, again and again. Notice the plot tracking the time on the x axisand the number of institution infected on the y axis. This is an estimate of the diffusion curve for the institution.
(6) To restart the simulation, click the Reinfect One button. Prior to hitting this button, slide theInfected Slider to any Law School you would like to observe. Also, feel free to adjust the p slider to increase or decrease the infectiousness of the idea.
Please comment if you have any difficulty or questions. Note you must have Java 1.4.1 + installed on your computer. The Information Technology professionals at many institutions will have already installed this on your machine but if not you will need to download it. We hope you enjoy!
The Forest Fire Model is a commonly invoked example of non-linear system–where a very small perturbation can generate significant differences in observed outcomes. Consider the above Netlogo–to Run the Model: (1) Adjust the Density Slider to set the concentration within the Forest. (2) Hit the Setup Button (3) Hit the Go Button …. Rinse and Repeat at different levels of Density.
Above is the output for a run of the model at several levels of Density {48%, 56%, 62%}. Notice the differences in the Percent Burned {1.6%, 5.2%, 86.5%}.
This is obviously a theoretical model but it has potential application to a wide class of substantive questions including regulatory failure. In addition, the Forest Fire Model is important because it has been invoked in the critique of the popular book The Tipping Point. Specifically, in discussing the book network scientist Duncan Watts notes “It sort of sounds cool … But it’s wonderfully persuasive only for as long as you don’t think about it.” Watts notes “…trends are more like forest fires: There are thousands a year, but only a few become roaring monsters. That’s because in those rare situations, the landscape was ripe: sparse rain, dry woods, badly equipped fire departments. If these conditions exist, any old match will do…. and nobody… will go around talking about the exceptional properties of the spark that started the fire.” (Quotes from Jan 2008 Is the Tipping Point Toast? Fast Company Magazine).