Last summer, Dan, Jon and I wrote our conference paper for ASNA 2009 entitled On the Stability of Community Detection Algorithms on Longitudinal Citation Data. The purpose of this paper was to experimentally explore a number of properties of community detection algorithms, especially as applied to citation networks (c.f. Supreme Court, Tax Court, United States Code).
The model is a fairly simple discrete-time directed growing graph. At time 0, we create a completely disconnected graph with some initial number of vertices. The number of new vertices after time 0 is then modeled by a homogeneous Poisson process. For each of these new vertices, we also model the number of edges per vertex as IID Poisson distributions. The probability distribution over these edges is specified by a modified preferential attachment mechanism.
Most of our questions consider what we’ve called the average pairwise stability. This can be thought of as answering the following question: “what is the probability that Alice and Bob are friends tomorrow if they were friends today?” Here, friendship corresponds to sharing the same community. By asking this question for all pairs of vertices (dyads) for all time steps in which both vertices existed, we get a probability that a community dyad is preserved from step to step. It is important to note that we’re not claiming all algorithms applied to all systems should have high average pairwise stability. In fact, for systems that involve dynamics like random rewiring, the only way to get high pairwise stability is to put all vertices in the same community or their own community at all steps – obviously trivial and unhelpful solutions in practice.
Given this model and this conception of stability, we want to perform the following experiments:
- How do the edge-betweenness, fast greedy, and leading eigenvector community detection algorithms compare in terms of their average pairwise stability…
- for varying levels of preferential attachment?
- for varying vertex and edge rates?
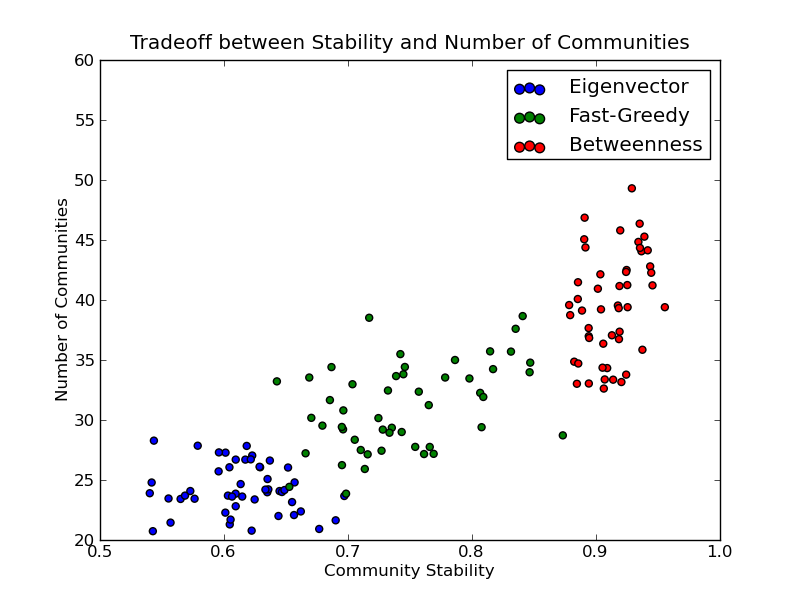
- Is there a significant tradeoff between the number of communities and the average pairwise stability of these community detection algorithms?
The answers are yes, yes, and yes! You should read the paper for more details.
I’ve also produced some code to help you assess the average pairwise stability for your dataset. The code requires igraph and is only in Python at this point due to an issue with R’s vertex label handling (which I can hopefully work around). You can get the average pairwise stability methods on github and check out the example below: