Today, I am traveling to Kansas for The Patent Conference (aka Pat Con). Tomorrow, I will be presenting our methods paper Distance Measure for Dynamic Citation Networks (published in the Statistical Mechanics Journal – Physica A in October 2010). While the specific applied example in paper is focused on case-to-case legal citations, the formalization and method we present therein has general form applicability to all dynamic direct acyclic graphs (including the patent citation network). Thus, we are interested in discussing how to leverage our approach to better understand the path of innovation that is revealed in datasets such as the NBER patent dataset.
Month: April 2011
Transportation in Contemporary Society: A Complex Systems Approach [Via MIT World]
.
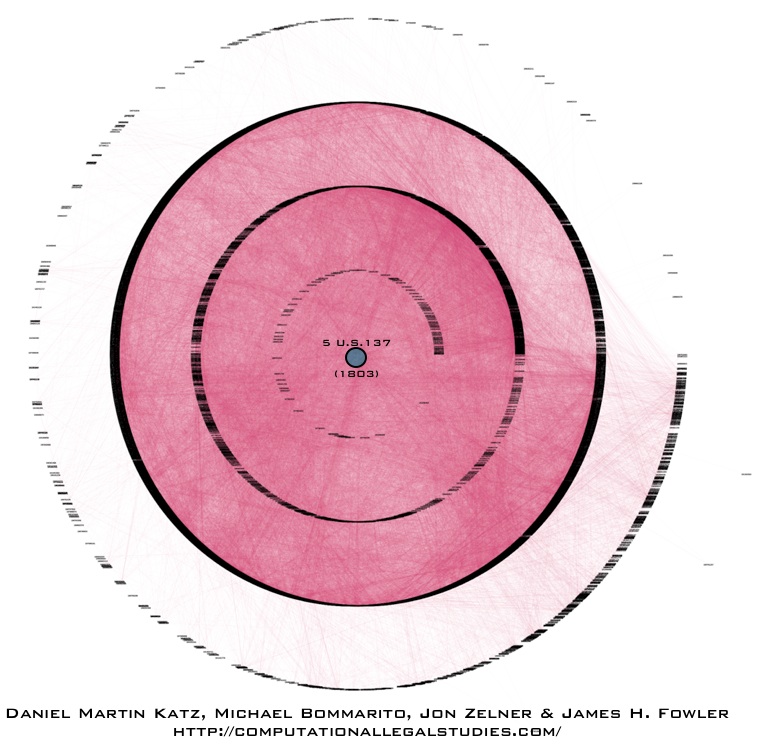
Six Degrees of Marbury v. Madison : A Sink Based Visualization [v2]
The visualization above is something we are calling the “six degrees” of Marbury v. Madison. It was originally produced for use in our paper Distance Measures for Dynamic Citation Networks. Due to space considerations, we ended up leaving it on the cutting room floor. However, the visual is designed to highlight the idea of a “sink.”
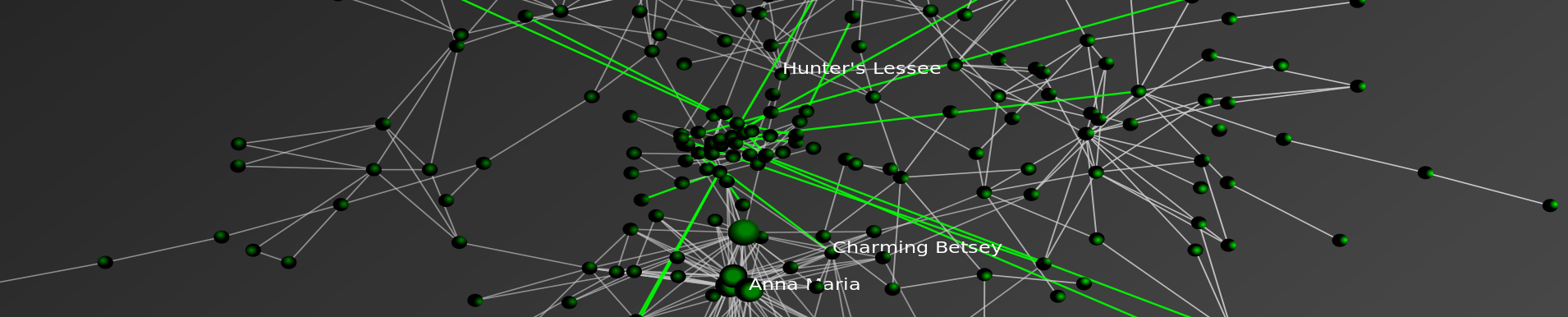
Sinks are one of the core concepts which we outline in Distance Measures for Dynamic Citation Networks, 389 Physica A 4201 (October 1 2010). Looking through the prism of a citation network, sinks are the root to which a given legal concept, academic idea or patent based innovation can be drawn. From each citation in a non-sink node, it is possible to trace the chains of citations back to their root (which we call a sink). In the visualization above, the root or sink node is the famed United States Supreme Court decision Marbury v. Madison. Starting from the center and working out to the edge, the first ring are cases that directly cite Marbury v. Madison. The next ring are cases which cite cases that cite Marbury v. Madison. The next ring are cases which cite cases which cases that cite Marbury v. Madison and so on…
Anyway, one of the major contributions of our Distance Measures for Dynamic Citation Networks paper is that it allows us to use these sinks to create pairwise distance/similarity measure between the ith and jth unit. In this instance, the units in this directed acyclic network are the ith and jth decisions of the United States Supreme Court.
Now, it is important to note cases contain many citations and thus can be oriented relative to many different sinks. So, even if a case can be traced to the Marbury sink – this does not preclude it from being traced to other sinks as well. Also, it is possible to construct a variety of mathematical functions to characterize the sink based distance between units. For instance, the importance of a sink might decay as its shortest path length increases. An alternative measure might weight the importance of each sinks by the number of unique ancestors shared between nodes i and j that are descended from a given sink of interest. Indeed, many fine-grained choices are possible but they require justification drawn from the given substantive problem.
As mentioned above, this method has potential applications including tracing the spread of technological innovation in patent citations or the spread of ideas in a set of academic articles. However, given our primary interest surrounds the judicial citations, we are working on the follow up to the “sinks” paper. In this follow up paper, we hope to carry these and other ideas forward into a definitive community detection method for judicial citation networks.
To preview, at least two major dynamics must be considered in any null model for community detection. First, case-to-case citations can help contribute to the fractal nature of legal systems. In other words, we are pretty far from any sort of gaussian null model. However, this is easy enough to confront with an alternative null — some highly skewed distribution (i.e. power law or power law with a cutoff, etc.)
 Here is the difficult part — the cross fertilization of legal concepts. This is a time evolving network where ideas are referenced/imported from otherwise unrelated or previously unrelated domains. The examples of cross-fertilization are numerous. One of my personal favorite non-SCOTUS examples is the use of the tort doctrine of “trespass to chattels” in the context of web scraping.
Here is the difficult part — the cross fertilization of legal concepts. This is a time evolving network where ideas are referenced/imported from otherwise unrelated or previously unrelated domains. The examples of cross-fertilization are numerous. One of my personal favorite non-SCOTUS examples is the use of the tort doctrine of “trespass to chattels” in the context of web scraping.
Anyway, we hope to have more to come on the topic of SCOTUS community detection in the weeks and months to come. In the meantime, please check out a Dynamic 3D Hi Definition United States Supreme Court Visualization.