Do legal systems have physical properties? Considered in the aggregate, do the distinctions upon distinctions developed by common law judges self-organize in a manner that can be said to have definable physical property (at least at a broad level of abstraction)? The answer might lie in fractal geometry.
Fractal geometry was developed in a set of classic papers by mathematician Benoît Mandelbrot. The original paper in the field How Long is the Coastline of Britain describes the coastline measurement problem. In short form, the length of the coast line is a function of the size of measurement one employs. As shown below, as the unit of measurement decreases the length of the coastline increases. The ideas expressed in this and subsequent papers have been applied to a wide class of substantive questions. In particular, the application to economic systems has been particularly illuminating. Given recent economic events, we agree with views of the Everyday Economist arguing the applied economic theory built upon his work should earn Mandelbrot a share of the Nobel Prize.
A more abstract fractal is the simple version of the Sierpinski triangle displayed at the top of this post. Here, there exists self similarity at all levels. Specifically, at each iteration of the model, the triangles at the tip of each of the lines replicate into self similar versions of the original triangle. If you click on the visual above, you can run the applet (provided you have java installed on your computer). {Side note: those of you NKS Wolfram fans out there will know the Sierpinski triangle can be generated using cellular automata Rule 90.}
For those who are interested in another demonstration consider the Koch Snowflake — a fractal which also offers a view of the relevant properties. The Koch Snowflake is a curve with infinite length (i.e. there is no convergence even though it is located in a bounded region around the original triangle). Click here to view an online demo of the Koch Snowflake.
So, you might be wondering … what is the law analog to fractals? As a first-order description of one important dynamic of the common law, we believe significant progress can be made by considering the conditions under which legal systems behave in a manner similar to fractals. For those interested, a number of important papers have discussed the fractal nature of legal systems. While discussing legal argumentation, the original idea is outlined in two important early papers The Crystalline Structure of Legal Thought and The Promise of Legal Semiotics both by Jack Balkin. The empirical case began more than ten years ago in the important paper How Long is the Coastline of the Law? Thoughts on the Fractal Nature of Legal Systems by David G. Post & Michael B. Eisen. It continues in more recent scholarship such as The Web of the Law by Thomas Smith.
In our view, the utility of this research is not to adjudicate the common law to be a fractal. Indeed, there exist mechanisms which likely prevent legal systems from actually behaving as unbounded fractal. The purpose of the discussion is determine whether describing law as a fractal is a reasonable first-order description of at least one dynamic within this complex adaptive system. While full adjudication of these questions is still an area of active research, we highlight these ideas for their important potential contribution to positive legal theory.
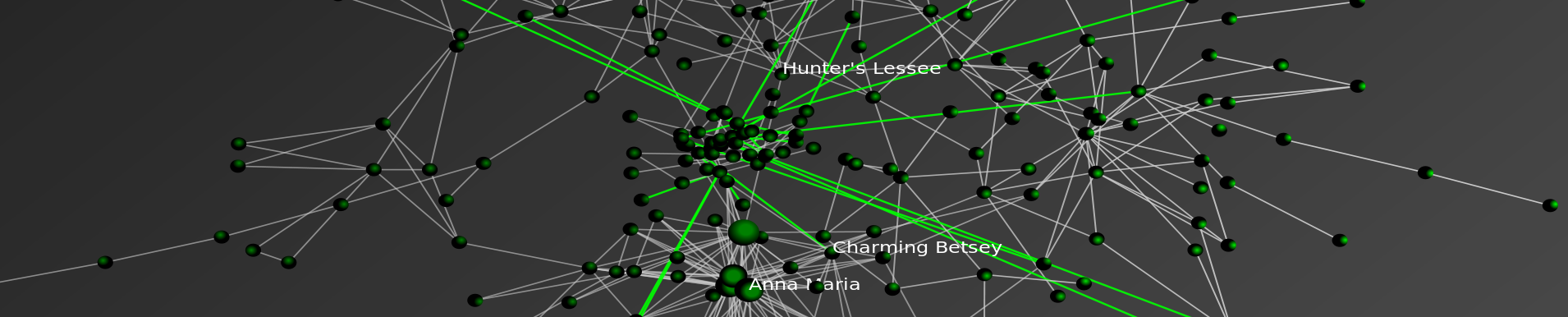
One thing we want to flag is the important relationship between the power law distributions we discussed in these prior posts (here and here) and the original work of Benoît Mandelbrot. The mapping of the power law like properties displayed by the common law and its constitutive institutions is part of the larger empirical case for the fractal nature of legal systems. Building upon the prior work, in two recent papers, which are available on SSRN here and here, we mapped this property of self organization among two sets of legal elites — judges and law professors.
